목차
1. 외적의 정의
외적(cross product)의 정의
2,3차 행렬식 (determinant of order 2 )의 계산, 외적의 행렬 계산법
2. 외적의 성질
벡터의 수직조건, 외적의 크기, 평행 조건, 평행사변형 넓이 (the area of the parallelogram)와 외적
3. 외적의 연산법칙과 계산
표준기저벡터의 외적
외적의 연산법칙
4. 스칼라 삼중적 (scalar triple product)
스칼라 삼중적 (scalar triple product)
평행육면체(parallelepiped)의 부피, 동일 평면 상에 있는 벡터(coplanar)
시작하기 전에
미분적분학을 공부하러 오신 분들 환영합니다!
저는 대학에 다니고 있는 대학생으로, 제가 공부했던 여러 학문 분야들의 내용을 정리하여 새로이 배우는 분들에게 더 쉬운 이해를 주고자 게시글을 작성하게 되었습니다!
대학과목 특성상 자료도 찾기 쉽지 않고 어렵기에 저도 공부하는데 많이 힘들었었는데, 다양한 예시와 그림들, 그리고 문제들과 설명을 통해 많은 내용을 전달하고자 합니다. 대학생 분들에게 많은 도움이 되었으면 좋겠습니다.
오늘은 벡터의 외적에 대해 알아보고자 합니다. Stewart 미분적분학 9E판을 참고하여 작성하였습니다. (CENGAGE 출판사)
*한국 교육과정 기준, 고등학교에서 나오는 수학 개념을 모두 안다고 가정하고 설명드리고 있습니다! 다만 필요시 이미 배운 내용이라도 다시 언급하고 있습니다.(특히 미적분, 기하, 확률과 통계로 나누어져 같은 이과여도 학습여부에 차이가 있어 고등학교 2학년 과정인 수학 I, II까지 안다고 가정하고 설명드리겠습니다!)
*설명은 한국어와 영어 표현을 모두 사용합니다. 문제 역시 모두 사용하였습니다.
외적의 정의
외적이란 무엇일까요? 외적의 정의를 이해하기 위해 도입한 이유부터 알아야겠죠.
외적은 두 벡터와 동시에 수직인 벡터를 정의하기 위해 만들었습니다.
즉, 영이 아닌 두 주어진 벡터 $\mathbf{a}=\left\langle a_1, a_2, a_3\right\rangle$ 과 $\mathbf{b}=\left\langle b_1, b_2, b_3\right\rangle$ 가 있다고 합시다.
이때 $\mathbf{a}$ 와 $\mathbf{b}$ 모두와 수직인 영벡터가 아닌 벡터 $\mathbf{c}$를 도입한 것이죠.
정의는 다음과 같습니다. 여러 가지 계산법이 있습니다. 식을 아예 외우셔도 좋고, 나중에 나오겠지만 행렬을 통해 계산하셔도 됩니다.
*곱하기 표기와 상당히 헷갈릴 수 있어 주의를 요합니다!
Def. 벡터의 정의
$\mathrm{a}=\left\langle a_1, a_2, a_3\right\rangle, \mathrm{b}=\left\langle b_1, b_2, b_3\right\rangle$ 일 때 a와 b의 외적(cross product) 은 다음과 같은 벡터입니다.
$$\mathbf{a} \times \mathbf{b}=\left\langle a_2 b_3-a_3 b_2, a_3 b_1-a_1 b_3, a_1 b_2-a_2 b_1\right\rangle$$
증명은 아래 더 보기를 눌러 확인하실 수 있습니다.
영벡터가 아닌 두 벡터 $\mathbf{a}=\left\langle a_1, a_2, a_3\right\rangle$ 과 $\mathbf{b}=\left\langle b_1, b_2, b_3\right\rangle$ 에 대해 영벡터가 아닌 벡터 $\mathbf{c}=\left\langle c_1, c_2, c_3\right\rangle$ 가 존재한다고 가정합시다.
$\mathbf{a}$ 와 $\mathbf{b}$ 모두와 벡터 $\mathbf{c}$가 수직이라 하면, 내적의 정의에 의해 $\cos(90)=0$이므로,
$\mathbf{a} \cdot \mathbf{c}=0$ 이고 $\mathbf{b} \cdot \mathbf{c}=0$ 입니다.
따라서 다음이 성립합니다. (내적 계산을 그대로 쓴 것입니다!)
$$
\begin{aligned}
& a_1 c_1+a_2 c_2+a_3 c_3=0 &---(1)\\
& b_1 c_1+b_2 c_2+b_3 c_3=0 &---(2)
\end{aligned}
$$
$c_3$ 를 소거하기 위해, 식 1에 $b_3$ 을 곱하고 식 2에 $a_3$ 을 곱한 후에 양변을 빼면
아래와 같은 결과를 얻습니다.
$$
\left(a_1 b_3-a_3 b_1\right) c_1+\left(a_2 b_3-a_3 b_2\right) c_2=0 ---(3)
$$
식 3 은 임의의 변수 $p, q$에 대해 $p c_1+q c_2=0$ 형태를 지니고 있습니다.
이때 이 식을 만족시킬 수 있는 $p, q$ 해 중 하나는 $c_1=q, c_2=-p$라고 볼 수 있습니다.
($pq-pq=0$이기 때문입니다!)
따라서 식 3의 해는 다음과 같습니다
$$
c_1=a_2 b_3-a_3 b_2, \quad c_2=a_3 b_1-a_1 b_3
$$
이 값들을 원래 식에 대입하여 $c_3$를 계산하면,
$$
c_3=a_1 b_2-a_2 b_1
$$
입니다.
따라서, $\mathbf{a}$ 와 $\mathbf{b}$ 에 모두 수직인 벡터는 아래와 같습니다.
$$
\left\langle c_1, c_2, c_3\right\rangle=\left\langle a_2 b_3-a_3 b_2, a_3 b_1-a_1 b_3, a_1 b_2-a_2 b_1\right\rangle
$$
이때 이 벡터를 $\mathbf{a}$ 와 $\mathbf{b}$ 의 외적이라 하며, 기호 $\mathbf{a} \times \mathbf{b}$ 로 나타냅니다.
두 벡터 $\mathbf{a}$ 와 $\mathbf{b}$ 의 외적 $\mathbf{a} \times \mathbf{b}$ 는 벡터임을 꼭 기억합시다!
벡터를 내적 하면 스칼라 값이 도출되었던 것과 반대로 외적 하면 벡터가 나옵니다!
그래서 이것을 벡터곱(vector product)이라고 부르기도 합니다.
다만 2차원 벡터에서 계산이 가능한 내적과 달리 외적 $\mathbf{a} \times \mathbf{b}$ 는 $\mathbf{a}$ 와 $\mathbf{b}$ 가 3차원 벡터일 때에만 정의됩니다!
아까 언급한 것과 같이, 행렬을 통해 식을 외우지 않고 빠른 계산이 가능합니다.
계산 과정을 소개하기 전에 2, 3차 행렬식(determinant of order 2,3)의 계산방법을 먼저 확인합시다.
Def. 2차 행렬식의 계산
2차 행렬식 (determinant of order 2 )은 다음과 같은 형태를 지니고, 계산은 대각선끼리 곱해서 빼는 과정을 거칩니다.
$$ \left|\begin{array}{ll}a & b \\c & d\end{array}\right|=a d-b c $$
예를 들면,
$$\left|\begin{array}{rr}2 & 1 \\-6 & 4\end{array}\right|=2(4)-1(-6)=14$$
와 같은 계산 과정을 거칩니다.
3차 행렬식은 2차 행렬식을 이용하여 아래와 같이 정의될 수 있습니다.
Def. 3차 행렬식의 계산
3차 행렬식 (determinant of order 3 )은 다음과 같은 형태를 가지고, 계산은 2차 행렬식을 활용하여 계산합니다.
$\left|\begin{array}{lll}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right|=a_1\left|\begin{array}{cc}b_2 & b_3 \\ c_2 & c_3\end{array}\right|-a_2\left|\begin{array}{cc}b_1 & b_3 \\ c_1 & c_3\end{array}\right|+a_3\left|\begin{array}{ll}b_1 & b_2 \\ c_1 & c_2\end{array}\right|$
외우실 때는 $a_1$, $a_3$에는 $+$, $a_2$에는 $-$를 붙인다, 그리고 각각 2차 행렬식을 계산한다! 이런 식으로 외우시면 편리합니다.
또한, 벡터의 경우 $a_1, a_2, a_3$자리에 모두 표준기저벡터가 들어가 있어서 계산이 훨씬 편합니다. (즉, 2차 행렬식이 각각 $x, y, z$성분이 되겠죠.
예를 들면,
$$\begin{aligned}
\left|\begin{array}{rrr}
1 & 2 & -1 \\
3 & 0 & 1 \\
-5 & 4 & 2
\end{array}\right| & =1\left|\begin{array}{ll}
0 & 1 \\
4 & 2
\end{array}\right|-2\left|\begin{array}{rr}
3 & 1 \\
-5 & 2
\end{array}\right|+(-1)\left|\begin{array}{rr}
3 & 0 \\
-5 & 4
\end{array}\right| \\
& =1(0-4)-2(6+5)+(-1)(12-0)=-38
\end{aligned}$$
처럼 계산이 가능합니다! 한번 따라 해 보세요.
이제 위 정의를 2 차 행렬식과 표준기저벡터 $\mathbf{i}, \mathbf{j}, \mathbf{k}$ 를 이용해서 다시 써 봅시다.
이 공식이 가장 자주 쓰입니다!
*$y$성분 계산에 마이너스가 붙는 사실을 잊지 마세요!!
Thm. 벡터의 외적(행렬 계산법)
$\mathbf{a}=a_1 \mathbf{i}+a_2 \mathbf{j}$ $+a_3 \mathbf{k}$ 와 $\mathbf{b}=b_1 \mathbf{i}+b_2 \mathbf{j}+b_3 \mathbf{k}$ 의 외적은 다음과 같다.
$$
\mathbf{a} \times \mathbf{b}=\left|\begin{array}{ll}
a_2 & a_3 \\
b_2 & b_3
\end{array}\right| \mathbf{i}-\left|\begin{array}{ll}
a_1 & a_3 \\
b_1 & b_3
\end{array}\right| \mathbf{j}+\left|\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right| \mathbf{k}
$$
*실제로는 3차원이지만 표준기저벡터를 사용하기 때문에, 굳이 3차원 행렬을 계산할 필요 없이 2차원 행렬만 계산해도 된다는 것이 장점입니다. 표준 표기는 아래와 같습니다. ( 위 식은 아래 식을 확장한 것입니다)
$$
\mathbf{a} \times \mathbf{b}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{array}\right|
$$
Tip
*예를 들어 $x$성분, 즉 표준기저벡터 $\mathbf{i} $ 를 계산할 경우,
$$\mathbf{a} \times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\a_1 & a_2 & a_3 \\b_1 & b_2 & b_3\end{array}\right|$$
에서 그 열을 제외하고 나머지 4칸을 계산하면 됩니다. 즉,
$$
\left|\begin{array}{ll}
a_2 & a_3 \\
b_2 & b_3
\end{array}\right|
$$
를 계산합니다.
이제 외적을 계산하는 예제를 한번 풀어봅시다!
더 보기를 눌러 해설을 확인하실 수 있습니다.
P1)
$\mathbf{a}=\langle 1,3,4\rangle, \mathbf{b}=\langle 2,7,-5\rangle$의 외적을 구하시오.
위에서 배운 공식을 그대로 활용하면 됩니다.
$$
\begin{aligned}
\mathbf{a} \times \mathbf{b} & =\left|\begin{array}{rrr}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & 3 & 4 \\
2 & 7 & -5
\end{array}\right| \\
& =\left|\begin{array}{rr}
3 & 4 \\
7 & -5
\end{array}\right| \mathbf{i}-\left|\begin{array}{rr}
1 & 4 \\
2 & -5
\end{array}\right| \mathbf{j}+\left|\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right| \mathbf{k} \\
& =(-15-28) \mathbf{i}-(-5-8) \mathbf{j}+(7-6) \mathbf{k}=-43 \mathbf{i}+13 \mathbf{j}+\mathbf{k}
\end{aligned}
$$
P2)
3차원 벡터공간 $V_3$ 의 임의의 벡터 $\mathbf{a}$ 에 대해 $\mathbf{a} \times \mathbf{a}=\mathbf{0}$ 임을 보이시오.
임의의 벡터이므로 성분을 미지수로 설정합시다.
$\mathbf{a}=\left\langle a_1, a_2, a_3\right\rangle$ 라 하고 외적 공식을 그대로 적용합시다.
$$
\begin{aligned}
\mathbf{a} \times \mathbf{a} & =\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_1 & a_2 & a_3 \\
a_1 & a_2 & a_3
\end{array}\right| \\
& =\left(a_2 a_3-a_3 a_2\right) \mathbf{i}-\left(a_1 a_3-a_3 a_1\right) \mathbf{j}+\left(a_1 a_2-a_2 a_1\right) \mathbf{k} \\
& =0 \mathbf{i}-0 \mathbf{j}+0 \mathbf{k}=\mathbf{0}
\end{aligned}
$$
가 되어 증명이 끝났습니다.
외적의 성질
이 파트에서는 외적의 여러 가지 성질들에 대해 알아보겠습니다!
총 4가지가 있습니다. 특히 외적의 크기는 중요한 내용이니 꼭 알아두시길 바랍니다.
Thm. 외적의 성질 1 - 벡터의 수직
벡터 $\mathbf{a} \times \mathbf{b}$ 는 $\mathbf{a}$ 와 $\mathbf{b}$ 에 모두 직교한다.
<증명 보기>
외적을 유도할 때부터 $\mathbf{a} \times \mathbf{b}$ 가 $\mathbf{a}$, $\mathbf{b}$ 와 수직인 것을 정의하고 계산을 했었습니다. 내적을 이용하여 재계산해 보겠습니다.
수직인 벡터끼리 내적 하면 $0$이 나오는 성질을 활용합니다.
따라서 $\mathbf{a} \times \mathbf{b}$ 와 $\mathbf{a}$를 내적 합니다.
$$
\begin{aligned}
(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{a} & =\left|\begin{array}{ll}
a_2 & a_3 \\
b_2 & b_3
\end{array}\right| a_1-\left|\begin{array}{ll}
a_1 & a_3 \\
b_1 & b_3
\end{array}\right| a_2+\left|\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right| a_3 \\
& =a_1\left(a_2 b_3-a_3 b_2\right)-a_2\left(a_1 b_3-a_3 b_1\right)+a_3\left(a_1 b_2-a_2 b_1\right) \\
& =a_1 a_2 b_3-a_1 b_2 a_3-a_1 a_2 b_3+b_1 a_2 a_3+a_1 b_2 a_3-b_1 a_2 a_3 \\
& =0
\end{aligned}
$$
비숫하게 계산하면 $(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{b}=0$ 임을 보일 수 있습니다.
따라서 $\mathbf{a} \times \mathbf{b}$ 는 $\mathbf{a}$ 와 $\mathbf{b}$ 에 모두 직교합니다.
두 번째 특징을 알아보기 전에, 외적의 방향에 대해 정의하고 갑시다!
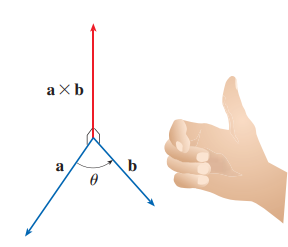
외적의 방향은, 표기 상 먼저 있는 벡터에서 나중에 나오는 벡터로 오른손을 써서 감싸면, 엄지손가락의 방향입니다.
위 그림을 참조하면 이해가 쉽습니다!
또한 사이 각 $\theta$를 통해 외적의 크기를 구할 수 있습니다.
이제 두 번째 특징인 외적의 크기에 대해 알아봅시다.
Thm. 외적의 특징 2- 외적의 크기(length of the cross product)
$\theta(0 \leq \theta \leq \pi)$ 가 $\mathbf{a}$ 와 $\mathbf{b}$ 사이의 각이면 다음이 성립한다.
$|\mathbf{a} \times \mathbf{b}|=|\mathbf{a}||\mathbf{b}| \sin \theta$
증명은 더보기를 눌러 확인하실 수 있습니다.
외적을 했을 때 외적된 벡터는,
$$\mathbf{a} \times \mathbf{b}=\left\langle a_2 b_3-a_3 b_2, a_3 b_1-a_1 b_3, a_1 b_2-a_2 b_1\right\rangle$$
와 같습니다.
따라서 이 벡터의 크기는,
$$
\begin{aligned}
|\mathbf{a} \times \mathbf{b}|^2= & \left(a_2 b_3-a_3 b_2\right)^2+\left(a_3 b_1-a_1 b_3\right)^2+\left(a_1 b_2-a_2 b_1\right)^2 \\
= & a_2^2 b_3^2-2 a_2 a_3 b_2 b_3+a_3^2 b_2^2+a_3^2 b_1^2-2 a_1 a_3 b_1 b_3+a_1^2 b_3^2
+a_1^2 b_2^2-2 a_1 a_2 b_1 b_2+a_2^2 b_1^2 \\
= & \left(a_1^2+a_2^2+a_3^2\right)\left(b_1^2+b_2^2+b_3^2\right)-\left(a_1 b_1+a_2 b_2+a_3 b_3\right)^2 \\
\end{aligned}$$
입니다.
이때, $|\mathbf{a}|^2=\left(a_1^2+a_2^2+a_3^2\right)$ 이고, $|\mathbf{b}|^2=\left(b_1^2+b_2^2+b_3^2\right)$입니다.
또한, $(\mathbf{a} \cdot \mathbf{b})=\left(a_1 b_1+a_2 b_2+a_3 b_3\right)$ 임을 이미 알고 있으므로,
$$
\begin{aligned}
= & |\mathbf{a}|^2|\mathbf{b}|^2-(\mathbf{a} \cdot \mathbf{b})^2 \\
= & |\mathbf{a}|^2|\mathbf{b}|^2-|\mathbf{a}|^2|\mathbf{b}|^2 \cos ^2 \theta \quad \\
= & |\mathbf{a}|^2|\mathbf{b}|^2\left(1-\cos ^2 \theta\right) \\
= & |\mathbf{a}|^2|\mathbf{b}|^2 \sin ^2 \theta
\end{aligned}
$$
임을 알 수 있습니다. ($\sin ^2 \theta+\cos ^2 \theta=1$)
양변에 제곱근은 씌우면,
$0 \leq \theta \leq \pi$ 일 때 $\sin \theta \geq 0$ 이므로 $\sqrt{\sin ^2 \theta}=\sin \theta$ 입니다.
따라서,
$$
|\mathbf{a} \times \mathbf{b}|=|\mathbf{a}||\mathbf{b}| \sin \theta
$$
가 됩니다.
세 번째 특징은 $\sin$함수를 생각해 보면 정말 당연하지만, 외적에서의 평행조건입니다.
Thm 3. 벡터 외적에서의 평행조건
영이 아닌 두 벡터 $\mathbf{a}$ 와 $\mathbf{b}$ 가 서로 평행(parallel)이기 위한 필요충분조건은 다음과 같다.
$\mathbf{a} \times \mathbf{b}=\mathbf{0}$
증명은 정말 간단합니다!
영이 아닌 두 벡터 $\mathbf{a}$ 와 $\mathbf{b}$ 가 서로 평행이기 위한 필요충분조건은 $\theta=0$ 또는 $\pi$ 입니다.(각도는 180도까지)
그런데 어느 경우이든 $\sin \theta=0$입니다.
따라서 $|\mathbf{a} \times \mathbf{b}|=0$ 이므로 $\mathbf{a} \times \mathbf{b}=\mathbf{0}$ 가 됩니다¡
이제 위 특징들을 통해서 외적의 크기와 방향을 모두 알았습니다¡
다시 한번 나열해보면、$\mathbf{a} \times \mathbf{b}$ 는 방향이 오른손 법칙으로 결정되고 길이(length)가 $|\mathbf{a}||\mathbf{b}| \sin \theta$ 이며, $\mathbf{a}$ 와 $\mathbf{b}$ 에 모두 수직인 벡터라고 말할 수 있습니다.
4번째 특징은 이를 기하학적으로 적용한 것입니다!
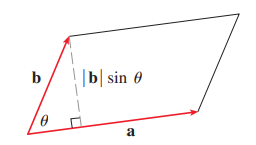
Thm. 외적과 평행사변형
두 벡터의 외적 $\mathbf{a} \times \mathbf{b}$ 의 크기(length)는 $\mathbf{a}$ 와 $\mathbf{b}$ 로 결정되는 평행사변형의 넓이(the area of the parallelogram)와 같다.
이번 증명은 그림에서도 알 수 있지만, 한번 더 설명하겠습니다.
아까 벡터의 크기가 $|\mathbf{a}||\mathbf{b}| \sin \theta$라고 했었습니다.
시점이 같은 두 벡터 $a$, $b$를 생각하면, 이는
$$
A=|\mathbf{a}|(|\mathbf{b}| \sin \theta)=|\mathbf{a} \times \mathbf{b}|
$$
와 같이 표현될 수 있습니다.
이때 $|\mathbf{a} \times \mathbf{b}|$는 평행사변형의 넓이와 같습니다.
따라서 시점을 같게 맞추면 평행사변형의 넓이와 같아집니다.
(벡터는 자유이동이 가능하므로 모든 벡터에 대해 적용 가능합니다.
P3)
(1) 세 점 $P(1,4,6), Q(-2,5,-1), R(1,-1,1)$ 을 지나는 평면에 수직인 벡터를 구하시오.
(2) 꼭짓점이 $P(1,4,6), Q(-2,5,-1), R(1,-1,1)$ 인 삼각형의 넓이를 구하시오.
Sol.

(1) 갑자기 평면? 당황할 수 있습니다. 그렇지만 평면 위의 두 벡터를 외적 하면, 그 평면에 수직인 벡터가 나온다는 사실을 알 수 있습니다. 즉,
벡터 $\overrightarrow{P Q} \times \overrightarrow{P R}$ 은 두 벡터 $\overrightarrow{P Q}$ 와 $\overrightarrow{P R}$ 에 모두 직교하고, 따라서 $P, Q, R$ 를 지나는 평면에 직교한다는 것입니다.(그림 참조해서 생각해 보세요!)
먼저 점을 사용하여 평면 위의 두 벡터를 구합니다.
$$
\begin{aligned}
& \overrightarrow{P Q}=(-2-1) \mathbf{i}+(5-4) \mathbf{j}+(-1-6) \mathbf{k}=-3 \mathbf{i}+\mathbf{j}-7 \mathbf{k} \\
& \overrightarrow{P R}=(1-1) \mathbf{i}+(-1-4) \mathbf{j}+(1-6) \mathbf{k}=-5 \mathbf{j}-5 \mathbf{k}
\end{aligned}
$$
그 후, 외적을 하면 끝입니다. 행렬을 사용해서 빠르게 해 봅시다.
$$
\begin{aligned}
\overrightarrow{P Q} \times \overrightarrow{P R} & =\left|\begin{array}{rrr}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
-3 & 1 & -7 \\
0 & -5 & -5
\end{array}\right| \\
& =(-5-35) \mathbf{i}-(15-0) \mathbf{j}+(15-0) \mathbf{k}=-40 \mathbf{i}-15 \mathbf{j}+15 \mathbf{k}
\end{aligned}
$$
가 됩니다.
cf) 직교하는 벡터를 구하라고 하였으므로 답으로 나온 벡터의 실수배는 모두 정답이 됩니다. 예를 들어
$\langle-8,-3,3\rangle$ 또한 평면과 수직입니다.
(2) 삼각형의 넓이는 평행사변형의 넓이의 반입니다.
또한 두 벡터를 외적한 크기는 평행사변형 넓이이므로, 위에서 구한 벡터
$$\overrightarrow{P Q} \times \overrightarrow{P R}=\langle-40,-15,15\rangle$$
의 크기를 구하면 됩니다.
$$
|\overrightarrow{P Q} \times \overrightarrow{P R}|=\sqrt{(-40)^2+(-15)^2+15^2}=5 \sqrt{82}
$$
으로부터, 삼각형의 넓이는 $\frac{1}{2}$를 곱하면 $\frac{5}{2} \sqrt{82}$가 됩니다.
외적의 연산법칙과 계산
외적에는 다양한 연산법칙들이 있습니다.
다만 몇 가지는 우리가 알던 계산 방식과 다른 것들이 있습니다.
먼저 표준기저벡터에 관해서 생각해 봅시다. 표준기저벡터끼리 외적 하면 어떻게 될까요?
Thm. 표준기저벡터의 외적
표준기저벡터 $\mathbf{i}, \mathbf{j}, \mathbf{k}$에 대해,
$$\begin {array}{}\mathbf {i} \times \mathbf {j}=\mathbf {k} & \mathbf {j}\times\mathbf{k}=\mathbf{i} & \mathbf{k} \times \mathbf{i}=\mathbf{j} \\
\mathbf{j} \times \mathbf {i}=-\mathbf {k} & \mathbf {k} \times \mathbf {j}=-\mathbf {i} &\mathbf {i} \times \mathbf {k}=-\mathbf {j} \\
\end {array}$$
쉽게 외우는 방법은 그냥 $\mathbf {i} -> \mathbf {j} -> \mathbf {k} -> \mathbf {i}$ 순으로 빙글 뱅글 돈다고 생각하시면 됩니다!
방향이 반대면 마이너스가 붙는다. 이렇게 생각하시면 편해요!
그런데, 위 식을 잘 보면
$$
\mathbf{i} \times \mathbf{j} \neq \mathbf{j} \times \mathbf{i}
$$
으로부터, 교환법칙이 성립하지 않음을 알 수 있습니다.
또한,
$$
\begin{aligned}
& \mathbf{i} \times(\mathbf{i} \times \mathbf{j})=\mathbf{i} \times \mathbf{k}=-\mathbf{j} \\
& (\mathbf{i} \times \mathbf{i}) \times \mathbf{j}=\mathbf{0} \times \mathbf{j}=\mathbf{0}
\end{aligned}
$$
으로부터, 결합법칙이 성립하지 않음을 알 수 있습니다. (즉, $(\mathbf{a} \times \mathbf{b}) \times \mathbf{c} \neq \mathbf{a} \times(\mathbf{b} \times \mathbf{c})$)
그래서 외적은 우리가 아는 대수적인 계산이 안 되는 경우가 많습니다.
그래도 몇 가지 자주 쓰이는 유효한 계산 방법을 아래를 보시면 알 수 있습니다!
Thm. 통상적으로 사용되는 외적의 연산 법칙
외적의 성질 $\mathbf{a}, \mathbf{b}, \mathbf{c}$ 가 벡터이고 $c$ 가 스칼라이면 다음이 성립한다.
1. $\mathbf{a} \times \mathbf{b}=-\mathbf{b} \times \mathbf{a}$
2. $(c \mathbf{a}) \times \mathbf{b}=c(\mathbf{a} \times \mathbf{b})=\mathbf{a} \times(c \mathbf{b})$
3. $\mathbf{a} \times(\mathbf{b}+\mathbf{c})=\mathbf{a} \times \mathbf{b}+\mathbf{a} \times \mathbf{c}$
4. $(\mathbf{a}+\mathbf{b}) \times \mathbf{c}=\mathbf{a} \times \mathbf{c}+\mathbf{b} \times \mathbf{c}$
5. $\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})=(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}$
6. $\mathbf{a} \times(\mathbf{b} \times \mathbf{c})=(\mathbf{a} \cdot \mathbf{c}) \mathbf{b}-(\mathbf{a} \cdot \mathbf{b}) \mathbf{c}$
모든 증명은 벡터를 성분으로 표현 한 뒤 연산하면 증명 가능합니다!
스칼라 삼중적(scalar triple product)
Def. 스칼라 삼중적
$\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})$ 를 벡터 $\mathbf{a}, \mathbf{b}, \mathbf{c}$ 의 스칼라 삼중적(scalar triple product)이라 한다.
이는 행렬식으로, 다음과 같이 표현이 가능하다.
$$
\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})=\left|\begin{array}{lll}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{array}\right|
$$
cf) $\mathbf{a} \times(\mathbf{b} \times \mathbf{c})$ 를 $\mathbf{a}, \mathbf{b}, \mathbf{c}$ 의 벡터 삼중적(vector triple product)이라 합니다.
스칼라 삼중적(scalar triple product)의 특징으로는, 위처럼 행렬식이 깔끔하게 떨어지는 형태가 나오는 게 있습니다.
또한, 스칼라 삼중적의 크기는 평행육면체(parallelepiped)의 부피와 같습니다.
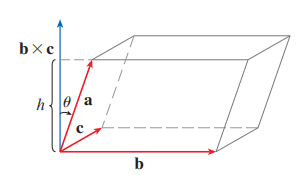
Thm. 평행육면체(parallelepiped)의 부피
벡터 $\mathbf{a}, \mathbf{b}, \mathbf{c}$ 로 결정되는 평행육면체의 부피는 다음과 같이 이들의 스칼라 삼중적(scalar triple product)의 크기이다.
$$
V=|\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})|
$$
Thm. 동일 평면 상에 있는 벡터(coplanar)
벡터 $\mathbf{a}, \mathbf{b}, \mathbf{c}$로 결정되는 평행육면체의 부피가 0 이면, 이 벡터들은 동일 평면 안에 있다고 한다.
증명은 더보기를 누르시면 확인하실 수 있습니다.
외적의 성질에 의해 평행사변형인 밑면의 넓이는 $A=|\mathbf{b} \times \mathbf{c}|$ 입니다.
$\theta$ 를 $\mathbf{a}$ 와 $\mathbf{b} \times \mathbf{c}$ 사이의 각이라 하면 평행육면체의 높이는 $h=|\mathbf{a}||\cos \theta|$ 가 됩니다. (이때 $\theta>\pi / 2$ 인 경우에는 $\cos \theta$ 대신에 $|\cos \theta|$ 를 이용해야 하기 때문에 절댓값이 들어갑니다). 따라서 평행육면체의 부피는 다음과 같습니다.
$$
V=A h=|\mathbf{b} \times \mathbf{c}||\mathbf{a}||\cos \theta|=|\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c})|
$$
P5)
스칼라 삼중적을 이용해서 터 $\mathbf{a}=\langle 1,4,-7\rangle, \mathbf{b}=\langle 2,-1,4\rangle, \mathbf{c}=\langle 0,-9,18\rangle$ 이 같은 평면에 있음(coplanar)을 보여라.
Sol.
이들의 스칼라 삼중적을 계산하면 다음과 같습니다.
$$
\begin{aligned}
\mathbf{a} \cdot(\mathbf{b} \times \mathbf{c}) & =\left|\begin{array}{rrr}
1 & 4 & -7 \\
2 & -1 & 4 \\
0 & -9 & 18
\end{array}\right| \\
& =1\left|\begin{array}{rr}
-1 & 4 \\
-9 & 18
\end{array}\right|-4\left|\begin{array}{rr}
2 & 4 \\
0 & 18
\end{array}\right|-7\left|\begin{array}{ll}
2 & -1 \\
0 & -9
\end{array}\right| \\
& =1(18)-4(36)-7(-18)=0
\end{aligned}
$$
이때 $\mathbf{a}, \mathbf{b}, \mathbf{c}$ 로 결정되는 평행육면체의 부피는 0 입니다. 이것은 $\mathbf{a}, \mathbf{b}, \mathbf{c}$가 동일 평면에 있음을 의미합니다.
수고하셨습니다! 다음 시간에는 직선과 평면의 방정식으로 찾아오겠습니다. 감사합니다.
다음 강의 보기
2024.08.11 - [기초공학과목/미분적분학(2)] - [미분적분학(2) 개념 정리] 11.5 (1) 직선의 방정식(equation of the line)
[미분적분학(2) 개념 정리] 11.5 (1) 직선의 방정식(equation of the line)
목차1. 직선의 방정식직선의 벡터 방정식, 매개변수방정식, 대칭방정식2. 선분(line segment)의 벡터방정식, 꼬인 위치(skew line)선분(line segment)의 벡터방정식두 직선의 위치 관계 확인시작하기 전에
azale.tistory.com



