목차
1. 벡터함수(Vector function)
벡터함수
벡터함수의 극한과 연속
2. 공간곡선(Space Curves)
공간곡선
증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니다.
벡터함수
우리가 잘 알고 있듯이 함수는 정의역의 각 원소를 치역의 한 원소에 대응시키는 규칙입니다.
벡터 함수(vector function) 또는 벡터값 함수(vector-valued function)는 같은 원리를 사용하지만, 정의역이 실수의 집합이고, 치역이 벡터의 집합인 함수입니다.
일반적으로 벡터함수
즉, 벡터함수
Thm. 벡터함수의 성분함수
벡터함수의 성분함수 (component function) 은 다음과 같다.
보통 독립변수로 문자
P1)
다음 벡터함수
또한 정의역은 각 함수에 대해 모두 생각하고, 교집합으로 합쳐야 합니다. 즉,
식
벡터함수의 극한과 연속
실수랑 똑같이 계산하면 됩니다.
Thm. 벡터함수의 극한
벡터함수
cf) 물론 벡터함수도 입실론-델타 논법을 활용하여 쓸 수도 있습니다.
실수에서의 연속과 마찬가지로 벡터함수에서도 연속조건이 존재합니다.
Thm. 벡터함수의 연속
다음을 만족할 매 벡터함수
즉,
P2 )
극한의 계산은 각 성분함수에 대해서 계산하면 끝입니다.
공간곡선
연속인 벡터함수와 공간곡선 사이에는 밀접한 관련이 있습니다.

Def. 공간곡선(Space curve)
위 방정식을
위 방정식을 잘 생각해보면
이제 아까 배운 벡터함수
즉, 벡터함수는 말 그대로 공간곡선 한 점 위로 가는 "벡터"를 나타내고, 공간곡선은 실제 그 곡선 자체를 의미합니다.
따라서 임의의 연속인 벡터함수
P3 )
벡터함수
2024.08.11 - [기초공학과목/미분적분학(2)] - [미분적분학(2) 개념 정리] 11.5 (1) 직선의 방정식(equation of the line)
대응하는 매개변수방정식은 다음과 같습니다.
이는 11.5장에서 배웠듯이 점
한편 이 함수는 다시 쓰면
평면곡선도 벡터기호로 표현할 수 있습니다.
예를 들면 매개변수방정식
P4)
벡터방정식이
(경험적인 문제입니다. 그림을 그려가면서 풀어보세요.)
cf) 위 벡터방정식 형태를 나선(helix)라 합니다.
이 곡선의 매개변수방정식은 다음과 같습니다.
삼각함수 공식 중에 적당한 공식을 사용합시다.
이 곡선은 원기둥
즉,
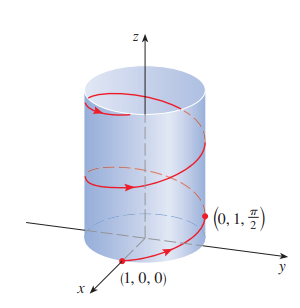
P5)
점
2024.08.11 - [기초공학과목/미분적분학(2)] - [미분적분학(2) 개념 정리] 11.5 (1) 직선의 방정식(equation of the line)
의 공식을 참조하세요.
11.5 절에서 배운 선분의 벡터 방정식은 다음과 같습니다.
여기서
이에 대응하는 매개변수방정식은 다음과 같습니다.
P6)
원기둥
(Hint :
적절한 매개변수
입니다.이때 주어진 평면의 방정식으로부터 다음을 얻을 수 있습니다.
따라서 모든 성분함수가 하나의 매개변수
이에 대응하는 벡터방정식은 다음과 같습니다.
6번과 같은 방법을 곡선
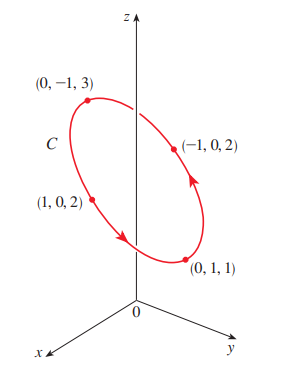
P7)
포물곡면
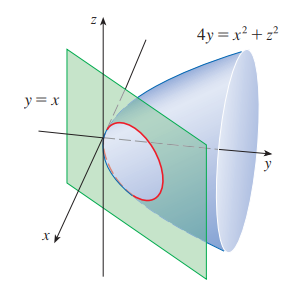
교선
따라서
을 얻을 수 있습니다.
이를 원의 형태로 만들기 위해
입니다.
따라서
위 예제랑 같은 방법으로,
입니다.
이 원은 중심이
앞과 같은 방법이지만 약간의 평행이동을 사용하여 매개변수화(parametrization)하면
로 쓸 수 있고,
입니다.
수고하셨습니다.
다음 시간에는 벡터함수의 도함수와 적분에 대해 알아보도록 하겠습니다.
감사합니다.
이전 강의 보기
[미분적분학(2) 개념 정리] 11.6 주면과 이차곡면 (Cylinders and Quadric Surfaces)
목차1. 주면(Cylinders)주면2. 이차곡면(Quadric Surfaces)이차곡면 증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니다.시작하기 전에미분적분학을 공부하러 오신 분들 환
azale.tistory.com
다음 강의 보기
[미분적분학(2) 개념 정리] 12.2 벡터함수의 도함수와 적분(Derivatives and Integrals of Vector Functions)
목차1. 벡터함수(Vector function)벡터함수벡터함수의 극한과 연속2. 공간곡선(Space Curves)공간곡선3. 예제 증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니다.벡터함수의
azale.tistory.com



