[미분적분학(2) 개념 정리] 12.2 벡터함수의 도함수와 적분(Derivatives and Integrals of Vector Functions)

 

 

목차

1. 벡터함수(Vector function)의 도함수, 단위접선벡터

벡터함수의 도함수 

단위접선벡터

2. 벡터함수의 미분 법칙

벡터함수의 미분 법칙

3. 벡터함수의 적분

벡터함수의 적분

4. 예제

 

증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니다.

---

벡터함수의 도함수(미분), 단위접선벡터

일반적인 스칼라 함수처럼 벡터함수도 당연히 미분과 적분이 가능합니다!

물론 연산 방식도 거의 동일합니다. 일반적인 함수처럼 미분계수의 정의를 이용하여 계산합니다.

저번 게시물에 언급을 안 했었는데, 보통 벡터함수의 경우 저렇게 볼드체를 사용합니다.

(손글씨로 쓸 때는 "lr(t)" 이렇게 그냥 한 줄 덧씌거나 진하게 칠하시면 됩니다.)

벡터함수의 도함수

Def. 벡터함수의 도함수

벡터함수 $\mathbf{r}$ 의 도함수(derivative) ${\mathbf{r}}^{\prime }$ 은 다음과 같다.
$$\frac{d\mathbf{r}}{dt}={\mathbf{r}}^{\prime }(t)=\underset{h\to 0}{lim}\frac{\mathbf{r}(t+h)-\mathbf{r}(t)}{h}$$

<증명>

위 그림처럼 점 $P$ 와 $Q$ 의 위치벡터가 $\mathbf{r}(t)$ 와 $\mathbf{r}(t+h)$라고 합시다.
이때 $\overrightarrow{PQ}$ 는 벡터 $\mathbf{r}(t+h)-\mathbf{r}(t)$ 를 나타내며 할선벡터(secant vector)가 됩니다.

만약 $h>0$ 이면 $(1/h)$ $(\mathbf{r}(t+h)-\mathbf{r}(t))$ 와 $\mathbf{r}(t+h)-\mathbf{r}(t)$ 는 같은 방향입니다.
따라서 $0$에 점점 가까워져서 $h\to 0$ 일 때 이 벡터는 접선 위 에 놓여 있는 벡터에 접근하는 것으로 나타난다.
미분계수의 정의에 따라 ${\mathbf{r}}^{\prime }(t)$ 가 존재하고,
${\mathbf{r}}^{\prime }(t)\ne 0$ 이면 벡터 ${\mathbf{r}}^{\prime }(t)$ 를 $\mathbf{r}$ 에 의해 정의되는 곡선의 점 $P$ 에서의 접선벡터(tangent vector)라 합니다.

$P$ 에서 $C$ 에 대한 접선(tangent line)은 $P$ 를 지나고, 접선벡터 ${\mathbf{r}}^{\prime }(t)$ 에 평행인 직선으로 정의됩니다.

또한 당연히, 벡터를 성분으로 다루는 것이 편리합니다.

따라서 벡터함수를 미분한다는 것은 곧 성분함수를 모두 미분한다는 것과 같습니다.

Thm. 벡터함수의 미분 방법

$f,g,h$가 주어진 정의역에서 모두 미분가능하다고 하면,

$\mathbf{r}(t)=⟨f(t),g(t),h(t)⟩=f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}$ 이면 다음이 성립한다.
$${\mathbf{r}}^{\prime }(t)=⟨f^{\prime }(t),g^{\prime }(t),h^{\prime }(t)⟩=f^{\prime }(t)\mathbf{i}+g^{\prime }(t)\mathbf{j}+h^{\prime }(t)\mathbf{k}$$

<증명>

모든 성분함수에 대해 미분계수의 정의를 입각하여 계산하면 아래와 같습니다.

$$\begin{array}{rl}{\mathbf{r}}^{\prime }(t)& =\underset{\mathrm{\Delta }t\to 0}{lim}\frac{1}{\mathrm{\Delta }t}[\mathbf{r}(t+\mathrm{\Delta }t)-\mathbf{r}(t)]\\ & =\underset{\mathrm{\Delta }t\to 0}{lim}\frac{1}{\mathrm{\Delta }t}[⟨f(t+\mathrm{\Delta }t),g(t+\mathrm{\Delta }t),h(t+\mathrm{\Delta }t)⟩-⟨f(t),g(t),h(t)⟩]\\ & =\underset{\mathrm{\Delta }t\to 0}{lim}⟨\frac{f(t+\mathrm{\Delta }t)-f(t)}{\mathrm{\Delta }t},\frac{g(t+\mathrm{\Delta }t)-g(t)}{\mathrm{\Delta }t},\frac{h(t+\mathrm{\Delta }t)-h(t)}{\mathrm{\Delta }t}⟩\\ & =⟨\underset{\mathrm{\Delta }r\to 0}{lim}\frac{f(t+\mathrm{\Delta }t)-f(t)}{\mathrm{\Delta }t},\underset{\mathrm{\Delta }\prime \to 0}{lim}\frac{g(t+\mathrm{\Delta }t)-g(t)}{\mathrm{\Delta }t},\underset{\mathrm{\Delta }t\to 0}{lim}\frac{h(t+\mathrm{\Delta }t)-h(t)}{\mathrm{\Delta }t}⟩\\ & =⟨f^{\prime }(t),g^{\prime }(t),h^{\prime }(t)⟩\end{array}$$

뒷 절(12.3)에서 나오는 내용인 곡률과 비틀림율 (curvature, torsion) 에서 정말 중요한 내용인

단위접선벡터(unit tangent vector)에 대해서도 알아야합니다! 이 정의는 정말 중요합니다.

"단위"라는 말에서 알 수 있듯 크기가 1이고 방향만 접선방향인 벡터를 말합니다.

 

즉 그냥 접선벡터를 접선벡터의 크기로 나눈 것입니다. (벡터의 크기는 각 성분을 제곱하고 합친 후 루트를 씌우면 됩니다.)

Def. 단위접선벡터(unit tangent vector)

접선벡터와 방향이 같은 단위 벡터를 단위접선벡터 $\mathbf{T}$ (unit tangent vector T)라고 하며 다음과 같이 정의한다.
$$\mathbf{T}(t)=\frac{{\mathbf{r}}^{\prime }(t)}{|{\mathbf{r}}^{\prime }(t)|}$$

---

벡터함수의 미분 법칙

 

벡터함수 역시 곱의 미분, 합성함수의 미분(Chain Rule) 등 스칼라 함수에서 사용했던 모든 연산법칙들을 사용 가능합니다.

Thm. 벡터함수의 미분법

$\mathbf{u}$ 와 $\mathbf{v}$ 를 미분가능한 백터함수, $c$ 를 스칼라, $f$ 를 실숫값 함수라 하면 다음이 성립한다.

1. 합의 미분

$\frac{d}{dt}[\mathbf{u}(t)+\mathbf{v}(t)]={\mathbf{u}}^{\prime }(t)+{\mathbf{v}}^{\prime }(t)$

2. 상수와 미분
$\frac{d}{dt}[c\mathbf{u}(t)]=c{\mathbf{u}}^{\prime }(t)$

3. 곱의 미분 (스칼라 함수와 벡터 함수)
$\frac{d}{dt}[f(t)\mathbf{u}(t)]=f^{\prime }(t)\mathbf{u}(t)+f(t){\mathbf{u}}^{\prime }(t)$

4. 곱의 미분 (벡터함수 끼리)

$\frac{d}{dt}[\mathbf{u}(t)\cdot \mathbf{v}(t)]={\mathbf{u}}^{\prime }(t)\cdot \mathbf{v}(t)+\mathbf{u}(t)\cdot {\mathrm{v}}^{\prime }(t)$

5. 곱의 미분 (외적된 벡터함수)
$\frac{d}{dt}[\mathbf{u}(t)\times \mathbf{v}(t)]={\mathbf{u}}^{\prime }(t)\times \mathbf{v}(t)+\mathbf{u}(t)\times {\mathbf{v}}^{\prime }(t)$

6. 합성함수 미분
$\frac{d}{dt}[\mathbf{u}(f(t))]=f^{\prime }(t){\mathbf{u}}^{\prime }(f(t))$
(Chain Rule)

 

위에서 알 수 있듯이 스칼라던지 벡터인지간에 관계없이 모두 연산이 가능함을 알 수 있습니다.

또한 잘 보시면 내적/외적도 미분 연산이 가능함을 알 수 있습니다.

사실 위 미분법의 모든 증명은 벡터함수를 성분함수로 쪼갠 다음에 연산하시면 됩니다.

아마 연습문제 같은 곳에 증명 문제가 있을 겁니다. (정말 귀찮습니다..)

---

또한 주목할 만한 정리가 하나 있습니다.

벡터함수의 도함수와 벡터함수의 직교조건

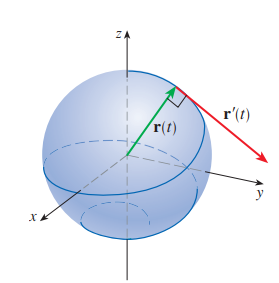
Thm. 벡터함수의 도함수와 벡터함수의 직교조건

$|\mathbf{r}(t)|=c$ (상수)이면 ${\mathbf{r}}^{\prime }(t)$ 는 모든 $t$ 에 대해 $\mathbf{r}(t)$ 와 직교한다.

$\mathbf{r}(t)\cdot \mathbf{r}(t)=|\mathbf{r}(t){|}^2=c^2$ 이고, $c^2$ 이 상수이므로, 위 공식중 내적 연산을 활용하면
$$0=\frac{d}{dt}[\mathbf{r}(t)\cdot \mathbf{r}(t)]={\mathbf{r}}^{\prime }(t)\cdot \mathbf{r}(t)+\mathbf{r}(t)\cdot {\mathbf{r}}^{\prime }(t)=2{\mathbf{r}}^{\prime }(t)\cdot \mathbf{r}(t)$$
입니다..
따라서 ${\mathbf{r}}^{\prime }(t)\cdot \mathbf{r}(t)=0$ 이고, ${\mathbf{r}}^{\prime }(t)$ 가 $\mathbf{r}(t)$ 에 직교임을 알 수 있습니다. (내적이 0이라는 것은 사잇각이 90도라는 의미입니다.)

---

벡터함수의 적분

스칼라 함수와 마찬가지로 벡터함수도 적분이 가능합니다.

사실 지금까지 나온 것들이 말이 벡터함수지 스칼라 함수랑 차이가 하나도 없기 때문에 난이도 자체는 매우 쉽습니다.

미분이랑 똑같이 각 성분함수에 대해 적분하면 됩니다.

또한 미적분학의 기본정리(Fundamental Theorem of Calculus)를 벡터함수에 대해서도 사용할 수 있습니다.

Thm. 벡터함수의 정적분(definite integral) 방법

$${\int }_a^b\mathbf{r}(t)dt=({\int }_a^{b}f(t)dt)\mathbf{i}+({\int }_a^{b}g(t)dt)\mathbf{j}+({\int }_a^{b}h(t)dt)\mathbf{k}$$

또는

$${{\int }_a^b\mathbf{r}(t)dt=\mathbf{R}(t)]}_a^b=\mathbf{R}(b)-\mathbf{R}(a)$$

증명은 스칼라 함수 정적분 방법과 똑같이 수열의 합을 통해 구할 수 있습니다.

$$\begin{array}{rl}{\int }_a^b\mathbf{r}(t)dt& =\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n\mathbf{r}\left(t_i^{\ast }\right)\mathrm{\Delta }t\\ & =\underset{n\to \mathrm{\infty }}{lim}[\left(\sum _{i=1}^{n}f\left(t_i^{\ast }\right)\mathrm{\Delta }t\right)\mathbf{i}+\left(\sum _{i=1}^{n}g\left(t_i^{\ast }\right)\mathrm{\Delta }t\right)\mathbf{j}+\left(\sum _{i=1}^{n}h\left(t_i^{\ast }\right)\mathrm{\Delta }t\right)\mathbf{k}]\end{array}$$

 

---

예제

P1.

(a) $\mathbf{r}(t)=(1+t^3)\mathbf{i}+t{e}^{-t}\mathbf{j}+\sin 2t\mathbf{k}$ 의 도함수(derivaitve)를 구하라.
(b) $t=0$ 인 점에서의 단위접선벡터(unit tangent vector)를 구하라.

(a) 그냥 바로 $\mathbf{r}$ 의 각 성분을 미분하면 됩니다.
$${\mathbf{r}}^{\prime }(t)=3t^2\mathbf{i}+(1-t)e^{-t}\mathbf{j}+2\cos 2t\mathbf{k}$$

(b) 먼저 해당 점에서의 $\mathbf{r}(0)$ 와 ${\mathbf{r}}^{\prime }(0)$을 구합시다.

즉 $t=0$ 을 대입하면 $\mathbf{r}(0)=\mathbf{i}$, ${\mathbf{r}}^{\prime }(0)=\mathbf{j}+2\mathbf{k}$ 이므로,

점 $(1,0,0)$ 에서의 단위접선벡터는 다음과 같습니다.
$$\mathbf{T}(0)=\frac{{\mathbf{r}}^{\prime }(0)}{|{\mathbf{r}}^{\prime }(0)|}=\frac{\mathbf{j}+2\mathbf{k}}{\sqrt{1+4}}=\frac{1}{\sqrt{5}}\mathbf{j}+\frac{2}{\sqrt{5}}\mathbf{k}$$

P2.

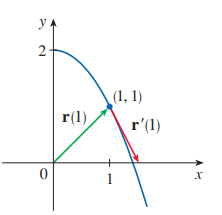
곡선 $\mathrm{r}(t)=\sqrt{t}\mathbf{i}+(2-t)\mathbf{j}$ 에 대해 ${\mathbf{r}}^{\prime }(t)$ 를 구하고, 위치벡터 $\mathbf{r}(1)$ 과 접선 벡터 ${\mathbf{r}}^{\prime }(1)$ 을 그리시오.

먼저 ${\mathbf{r}}^{\prime }(t)$는 그냥 미분함으로써 구할 수 있습니다. 그리고 ${\mathbf{r}}^{\prime }(1)$는 그냥 $t=1$을 대입하면 됩니다.

그러면
$\begin{array}{lll}& {\mathbf{r}}^{\prime }(t)=\frac{1}{2\sqrt{t}}\mathbf{i}-\mathbf{j},& {\mathbf{r}}^{\prime }(1)=\frac{1}{2}\mathbf{i}-\mathbf{j}\end{array}$

입니다.

 

방정식 $x=\sqrt{t},y=2-t$ 에서 적절히 매개변수를 소거하면 $y=$ $2-x^2,x\ge 0$ 을 얻을 수 있습니다.

이로써 해당 점은 $(1,1)$임을 알 수 있습니다.

위치벡터 역시 처음 주어진 식에 $t=1$를 대입하면 $\mathbf{r}(1)=\mathbf{i}+\mathbf{j}$ 입니다.

P2

 

P3.

매개변수방정식이 다음과 같은 나선에 대해 점 $(0,1,\pi /2)$ 에서 접선의 매개 변수방정식을 구하라.
$$x=2\cos t,y=\sin t,z=t$$

(Hint : 접선도 결국 직선이므로 방향수(기울기)와 한 점을 알고 있으면 매개변수 방정식은 바로 구할 수 있습니다. 그런데 한 점은 이미 알고 있고.. 그럼 기울기 벡터만 알아내면 되는데..?)

 

나선의 벡터방정식이 $\mathbf{r}(t)=⟨2\cos t,\sin t,t⟩$ 이므로
그냥 미분하면 도함수를 알 수 있습니다.
$${\mathbf{r}}^{\prime }(t)=⟨-2\sin t,\cos t,1⟩$$

점 $(0,1,\pi /2)$ 에 대응되는 매개변수의 값을 구해야 합니다.
그런데 $z=t$이므로 바로 $t=\pi /2$로 결정됩니다.
이때 $t=\pi /2$에서의 접선벡터는 값을 대입하면 ${\mathbf{r}}^{\prime }(\pi /2)=⟨-2,0,1⟩$입니다.

따라서 구하는 직선은 점 $(0,1,\pi /2)$ 를 지나고 벡터 $⟨-2,0,1⟩$ 에 평행인 직선입니다. 따라서 직선의 매개변수방정식 공식에 따라서 답은 다음과 같습니다.
$$x=-2t,y=1,z=\frac{\pi }{2}+t$$

P4. $\mathbf{r}(t)=2\cos t\mathbf{i}+\sin t\mathbf{j}+2t\mathbf{k}$ 라고 하자.
${\int }_0^{\pi /2}\mathbf{r}(t)dt$를 구하시오.

먼저 각 성분함수에 대해 부정적분을 구해봅시다.
$$\begin{array}{rl}\int \mathbf{r}(t)dt& =(\int 2\cos tdt)\mathbf{i}+(\int \sin tdt)\mathbf{j}+(\int 2tdt)\mathbf{k}\\ & =2\sin t\mathbf{i}-\cos t\mathbf{j}+t^2\mathbf{k}+\mathbf{C}\end{array}$$

정적분을 하면 적분상수는 사라지므로 정적분 하면
$$\begin{array}{rl}{\int }_0^{\pi /2}\mathbf{r}(t)dt& ={[2\sin t\mathbf{i}-\cos t\mathbf{j}+t^2\mathbf{k}]}_0^{\pi /2}\\ & =2\mathbf{i}+\mathbf{j}+\frac{{\pi }^2}{4}\mathbf{k}\end{array}$$

입니다.

---

읽어주셔서 감사합니다.

다음 게시물은 12단원에서 제일 복잡하고 외울 거 많은 단원이네요.

 

이전 강의 보기

[미분적분학(2) 개념 정리] 12.1 벡터함수와 공간곡선(Vector Functions and Space Curves)

 

다음 강의 보기

[미분적분학(2) 개념 정리] 12.3 (1) 호의 길이, 호의 길이함수, 매개변수화, 곡률 (Arc Length, Arc Length