목차
곡면에 작용하는 정수력(hydrostatic force acting on a curved surface)
오늘은 곡면에 작용하는 정수력(hydrostatic force acting on a curved surface)에 대해 알아보고자 합니다. 유체역학 SI Version Munson 저 6판을 참고하여 작성하였습니다. (CENGAGE 출판사)
곡면에 작용하는 정수력
전 시간까지 계속 반복했던 합력의 크기와 방향을 구하기 위해서 유도된 식들은 오직 평면일 경우에만 적용 가능합니다.
그러나 실제로 많이 사용되는 표면들은 평면이 아니고 보통 곡면입니다.
물론 평면의 경우와 같이 합력은 적분하여 구할 수 있지만, 이 과정은 일반적으로 유도될 수 없습니다.
(일반적인 식을 구할 수 없다는 뜻입니다.)
그 대안으로 곡면과 곡면의 수평 및 수직 투영면으로 둘러싸인 유체 체적의 평형을 고려해 보겠습니다.
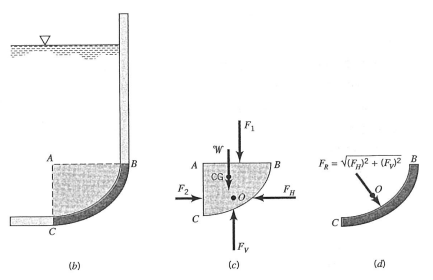
위 그림을 예로 듭시다. 왼쪽 그림에서 곡면 $B C$에 가해지는 합력을 구해 봅시다.
먼저 곡면 $B C$, 수평면 $A B$, 그리고 수직면 $A C$ 로 둘러싸인 유체체적을 분리합니다.
분리하면 가운데 그림과 오른쪽 그림처럼 분리가 됩니다. 먼저 가운데 그림을 봅시다.
자유 물체도를 보면, 1. 힘 $F_1$ 과 $F_2$ 의 크기와 위치는 평면에 대한 관계식으로부터 얻을 수 있습니다.
왜일까요? 저 둘은 곡선이 아니라 직선이기 때문입니다.
2. 무게 $\mathscr{W}$ 는 단순히 유체의 비중량과 유체체적을 곱한 값입니다.
(자주 했지만, 다시 언급하자면 밀도의 정의 $\rho times V = m$ 으로부터 $\rho times V times g = mg$ 이므로 $\gamma V = W$ 입니다!)
유체체적의 무게는 당연하겠지만 무게중심 중심 $(C G)$ 에 작용합니다.
3. 곡면에서의 힘 $F_H$ 와 $F_V$ 는 탱크가 유체체적에 가하는 힘의 성분들을 나타냅니다.
이로써 작용하는 모든 힘을 따져보았습니다.
이 계가 평형을 이루기 위해서는 수평 성분 $F_H$ 가 $F_2$ 와 크기가 같고 동일 선상에 있어야 하며,
수직 성분 $F_V$ 는 $F_1$ 과 $\mathscr{W}$ 의 합력과 크기가 같고 동일 선상에 있어야 합니다.
이것은 유체에 작용하는 세 힘( $F_2, F_1$ 과 $\mathcal{W}$ 의 합력, 탱크가 유체에 가하는 합력)이 공점력 계(concurrent force system)를 형성해야 하기 때문입니다. (어렵게 생각하실 필요 없이 그냥 "힘의 평형" 을 쓴 겁니다)

따라서
$$
\begin{aligned}
& F_H=F_2 \\
& F_V=F_1+\mathscr{W}
\end{aligned}
$$
이고, 합력의 크기는 아래의 식에서 구할 수 있습니다. (합력을 벡터 분해했다고 생각하시면 됩니다.)
$$
F_R=\sqrt{\left(F_H\right)^2+\left(F_V\right)^2}
$$
합력 $F_R$ 은 $O$ 를 지나며, 이 점의 위치는 적절한 축에 대하여 모멘트를 더하여 얻을 수 있습니다.
곡면 $B C$ 에 가해지는 유체의 합력은 가운데 그림의 자유물체도에서 얻은 합력의 크기와 같고 방향은 반대이다. 구하고자 하는 유체의 합력은 오른쪽 그림에 나와 있습니다.
곡면은 일반적인 방정식을 구할 수가 없어서 이렇게 하는 것이 학부 수준에서는 최대인 것 같습니다.
cf) 이와 같은 방법은 가압된 밀폐탱크의 곡면에 작용하는 힘을 구하는 데도 사용될 수 있습니다. 탱크에 기체가 채워져 있다면, 기체의 무게는 압력에 의한 험과 비교할 때 보통 무시될 수 있습니다. 따라서 곡면의 수평과 수직 투영면에 작용하는 힘(그림 $2.23 c$ 의 $F_1$ 과 $F_2$ 같은)은 내부압력과 투영면적의 곱으로 간단히 표현됩니다.
이전 강의 보기
[유체역학 개념정리] 2.8 압력프리즘(pressure prism)
목차압력프리즘(pressure prism)1. 압력프리즘(pressure prism) 12. 압력프리즘(pressure prism) 2 - 수직 직사각형면(유체표면 X)3. 압력프리즘(pressure prism) 3 - 경사진 평면4. 잠긴 평면에 대한 대기압의 영향5.
azale.tistory.com
다음 강의 보기
'고전역학 > 유체역학' 카테고리의 다른 글
| [유체역학 개념정리] 2.8 압력프리즘(pressure prism) (0) | 2024.08.18 |
|---|---|
| [유체역학 개념정리] 2.7 평면에 작용하는 정수력(hydrostatic force acting on a plane) (0) | 2024.08.17 |
| [유체역학 개념정리] 2.6 액주계(manometer) (0) | 2024.08.15 |
| [유체역학 개념정리] 2.5 압력의 측정(pressure measurement) (0) | 2024.08.14 |
| [유체역학 개념정리] 2.4 표준대기(standard atmosphere) (0) | 2024.08.14 |



