목차
표준대기
1. 표준대기
2. 온도가 변하는 과정에서 압축성 유체(기체)의 압력 분포
오늘은 표준대기(standard atmosphere)에 대해 알아보고자 합니다. 유체역학 SI Version Munson 저 6판을 참고하여 작성하였습니다. (CENGAGE 출판사)
표준대기
[유체역학 개념정리] 2.3 정지된 유체 내의 압력 분포 (pressure distribution in a stationary fluid )
목차정지된 유체 내의 압력 분포(1) 정지된 유체 내의 압력 분포 (2) 비압축성유체(액체 등)의 높이에 따른 압력 분포 (1)(3) 비압축성유체(액체 등) 의 높이에 따른 압력 분포 (2)(3) 압축성 유체오늘
azale.tistory.com
저번 시간에 배웠던 압축성 유체의 압력 분포에 관한 식
$$
\int_{p_1}^{p_2} \frac{d p}{p}=-\frac{g}{R} \int_{z_1}^{z_2} \frac{d z}{T}
$$
은 대기권을 다룰 때도 정말 중요합니다.
특히 중요한 적용 예는 지구 대기권에서의 압력 변화입니다.
압력을 구하고자 하는 특정 조건(온도, 기준압력)에서 특정 범위의 고도에 대한 압력의 값들을 가지는 것이 이상적입니다. 이를 위해 항공기, 미사일, 그리고 우주선을 설계하고 표준조건에서 이들의 성능을 비교하는 데 사용될 수 있는 '표준대기(standard atmosphere)'가 만들어졌습니다.
표준대기의 개념은 1920 년대에 처음 발표되었습니다. 그 이후 많은 국내 및 국제 위원회와 기구들이 표준을 수정하며 현재 채택된 표를 만들었습니다. 여기에는 지구 대기의 중간 위도에서의 연평균 상태를 이상적으로 나타낸 이른 바 미국 표준대기(U.S. standard atmosphere)가 있습니다.
해수면(sea level)에서 표준대기에 대한 여러 성질은 다음 표와 같습니다.
$$
\begin{aligned}
&\begin{array}{|c|c|}
\hline \text { 성질 } & \text { SI 단위 } \\
\hline \text { 온도, } T & 288.15 \mathrm{~K}\left(15^{\circ} \mathrm{C}\right) \\
\hline \text { 압력, } p & 101.33 \mathrm{kPa} \text { (abs) } \\
\hline \text { 밀도, } \rho & 1.225 \mathrm{~kg} / \mathrm{m}^3 \\
\hline \text { 비중량, } \gamma & 12.014 \mathrm{~N} / \mathrm{m}^3 \\
\hline \text { 점성, } \mu & 1.789 \times 10^{-5} \mathrm{~N} \cdot \mathrm{s} / \mathrm{m}^2 \\
\hline
\end{array}\\
&\text { * 해수면에서의 중력가속도 }=9.807 \mathrm{~m} / \mathrm{s}^2 \text {. }
\end{aligned}
$$
또한 아래 그림은 미국 표준대기의 온도 분포를 보여 줍니다.
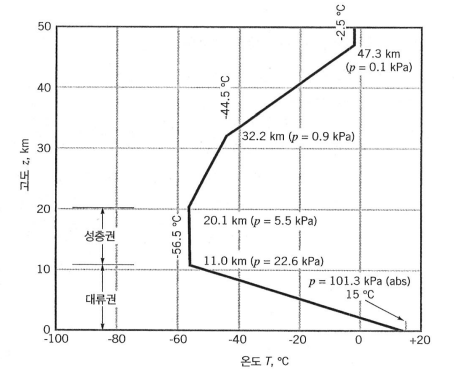
이 그림에서 볼 수 있듯이 지구 표면에 가장 가까운 대류권(troposphere)에서는 고도가 증가함에 따라 온도가 감소하고, 그다음 층인 성층권(stratosphere)에서는 온도가 거의 일정 하게 되며 그다음 층에서는 온도가 증가하기 시작합니다.
(아마 고등학교 과학 시간에도 비슷한 그림을 본 적이 있을 겁니다..)
온도가 변하는 과정에서 압축성 유체(기체)의 압력 분포
저번 차시에는 등온조건을 가정하여 식
$$
\int_{p_1}^{p_2} \frac{d p}{p}=-\frac{g}{R} \int_{z_1}^{z_2} \frac{d z}{T}
$$
를 적분했었는데, 이번에는 일반적으로 온도가 변화는 과정을 도입해 볼 겁니다.
온도의 변화가 위 표준대기 그림처럼 직선들로 표시되었습니다.
따라서 이를 적절히 표현하면 식을 적분하는 것이 가능합니다.
대류권에서 온도 변화는, (지표면에서 $11km$까지 적용 가능합니다. 대부분의 문제는 아래 식 사용)
$$
T=T_a-\beta z
$$
입니다.
(여기에서 $T_a$ 는 해수면 $(z=0)$ 에서의 온도이고 $\beta$ 는 온도감소율(lapse rate), 대류권의 표준대기에서는 $\beta=0.00650 \mathrm{~K} / \mathrm{m}$ 로 상수값.)
이를 식에 대입하여 적분하면
Thm. 온도가 변하는 과정에서 압축성 유체(기체)의 압력 분포(대류권, 약 11km까지)
$$
p=p_a\left(1-\frac{\beta z}{T_a}\right)^{g / R \beta}
$$
(여기서 $p_a$ 는 $z=0$ 에서의 절대압력, $p_a, T_a, g$ 는 각각 해수면에서 기준압력, 기준온도, 중력가속도(*위 표에 있는 값입니다. )/ 기체상수 $R=286.9$ $\mathrm{J} / \mathrm{kg} \cdot \mathrm{K}$ )
를 얻을 수 있습니다.
위 식을 사용하면 대류권 전체에 대한 압력 변화를 구할 수 있습니다.
예를 들어 이 계산에 의하면 온도가 $-56.5^{\circ} \mathrm{C}(217 \mathrm{~K})$ 인 대류권의 최상부에서는 절대압력이 약 23 kPa 이 됩니다.
수고하셨습니다.
다음 시간에는 압력의 측정에 대해 알아보겠습니다.
이전 강의 보기
[유체역학 개념정리] 2.3 정지된 유체 내의 압력 분포 (pressure distribution in a stationary fluid )
목차정지된 유체 내의 압력 분포(1) 정지된 유체 내의 압력 분포 (2) 비압축성유체(액체 등)의 높이에 따른 압력 분포 (1)(3) 비압축성유체(액체 등) 의 높이에 따른 압력 분포 (2)(3) 압축성 유체오늘
azale.tistory.com
다음 강의 보기
[유체역학 개념정리] 2.5 압력의 측정(pressure measurement)
목차표준대기1. 표준대기2. 온도가 변하는 과정에서 압축성 유체(기체)의 압력 분포오늘은 표준대기(standard atmosphere)에 대해 알아보고자 합니다. 유체역학 SI Version Munson 저 6판을 참고하여 작성하
azale.tistory.com
'고전역학 > 유체역학' 카테고리의 다른 글
| [유체역학 개념정리] 2.6 액주계(manometer) (0) | 2024.08.15 |
|---|---|
| [유체역학 개념정리] 2.5 압력의 측정(pressure measurement) (0) | 2024.08.14 |
| [유체역학 개념정리] 2.3 정지된 유체 내의 압력 분포 (pressure distribution in a stationary fluid ) (0) | 2024.08.14 |
| [유체역학 개념정리] 2.2 압력장에 대한 기본 방정식 (the basic equation for the pressure field) (0) | 2024.08.13 |
| [유체역학 개념정리] 2.1 한 점에서의 압력, 파스칼의 법칙 (pressure at a point, Pascal's Law) (0) | 2024.08.12 |



