[유체역학 개념정리] 2.8 압력프리즘(pressure prism)

목차

압력프리즘(pressure prism)

1. 압력프리즘(pressure prism) 1

2. 압력프리즘(pressure prism) 2 - 수직 직사각형면(유체표면 X)

3. 압력프리즘(pressure prism) 3 - 경사진 평면

4. 잠긴 평면에 대한 대기압의 영향

5. 예제

오늘은 압력프리즘(pressure prism) 에 대해 알아보고자 합니다. 유체역학 SI Version Munson 저 6판을 참고하여 작성하였습니다. (CENGAGE 출판사)

---

압력프리즘(pressure prism) 1

압력프리즘(pressure prism)

 

사각형 평면에 작용하는 유체의 힘에 대한 유익한 도식적 방법이 있습니다.

비중량이 $\gamma$ 인 액체 가 들어 있는 폭이 $b$ 인 탱크의 수직벽에 가해지는 압력분포를 생각해 봅시다.

왼쪽 그림은 정면, 오른쪽 그림은 입체적으로 표현한 것입니다.

 

먼저 압력은 깊이에 대하여 선형으로 변하므로 그림 $2.19 a$ 와 같은 압력분포를 가지며,

항상 써왔던 비압축성 유체의 높이와 압력에 따른 공식을 사용하면,

위 표면에서의 압력은 $0$ 이고 바닥에서의 압력은 $\gamma h$ 입니다.

 

이 그림으로부터 평균압력(압력의 반)은 깊이가 $h / 2$ 인 위치에서의 압력인 것을 알 수 있으므로

$$p_{\mathrm{av}} A= \gamma\left(\frac{h}{2}\right)$$

 

겠죠? 또한 사각형의 면적 $A=b h$ 에 작용하는 합력은, 압력의 정의 $P=F/A$에 의해,

$$
F_R=p_{\mathrm{av}} A=\gamma\left(\frac{h}{2}\right) A
$$

이며 평면에 작용하는 정수력으로부터 얻은 결과와 같습니다.

아래 글 참조하세요!

[유체역학 개념정리] 2.7 평면에 작용하는 정수력(hydrostatic force acting on a plane)

 

어쨌든 왼쪽 그림의 압력분포는 수직면 전체에 적용되므로 오른쪽 그림과 같이 3 차원 압력분포를 그릴 수 있습니다.

각 점에서의 높이(화살표)는 압력입니다. 또한 이 압력선으로 이루어진 도형이 생기죠? 이때 이 도형의 부피, 즉

이 체적을 압력프리즘(pressure prism)이라 부르며, 사각형 평면에 작용하는 합력은 압력프리즘의 체적과 같습니다.

그러니까 한마디로 부피는 결국 합력과 관련있다는 뜻입니다. 앞 단원 정수력 파트에서 배웠던 합력을 구하는 다른 방법을 알아보는 겁니다!

 

따라서 위 프리즘에서 유체에 의한 힘은
$$
F_R=V(\text { volume })=\frac{1}{2}(\gamma h)(b h)=\gamma\left(\frac{h}{2}\right) A
$$
이고, 여기에서 $b h$ 는 사각형 평면의 면적 $A$ 입니다.

합력은 압력프리즘의 도심을 지나야 한다. 즉, 합력이 지나는 지점은 $h_c$, $y_c$가 아닙니다.

 

따라서 합력의 작용점은 밑면에서 $h / 3$ 위에 있습니다(삼각형의 도심이 밑변에서 $h / 3$ 위에 있으므로).

이 결과는 저번 시간 2.7에서 배운 식과 일치함을 알 수 있습니다.

---

압력프리즘(pressure prism) 2 - 수직 직사각형면(유체표면 X)

수직 직사각형면에 작용하는 정수력

이러한 도식적인 접근방법은 위 그림과 같이 평면이 유체표면까지 연장되지 않을 때(즉, 평면이 대기까지 안 닿을 때, 왼쪽 그림 참고)에도 사용될 수 있습니다. 이 경우 압력프리즘의 단면은 사다리꼴이 되겠죠? 

 

그러나 무슨 도형이던 합력은 여전히 압력프리즘의 체적과 같으며 체적의 도심을 지납니다.

이 압력프리즘을 오른쪽 그림과 같이 사각형 $A B D E$ 와 삼각형 $B C D$ 의 두 부분으로 나누면
$$
F_R=F_1+F_2
$$

로 표현할 수 있습니다. 각 성분은 항상 하던대로 2.7절에서 배운 합력공식을 써서 쉽게 구할 수 있습니다.

 

또한, $F_R$ 의 작용점 위치는 $A$ 를 지나는 축과 같은 임의의 축에 대해 모멘트를 더하여 구할 수 있습니다. 이 경우
$$
F_R y_A=F_1 y_1+F_2 y_2
$$
가 됩니다. (모멘트를 합칠 때, 정역학 참고)

$y_1$ 과 $y_2$ 는 쉽게 구할 수 있는 값들이겠죠? (그냥 도심의 좌표)

---

압력프리즘(pressure prism) 3 - 경사진 평면

경사진 평면에서 압력프리즘

 

 

경사진 평면에서도 압력프리즘의 방법이 적용되며 이때 프리즘의 단면은 위 그림과 같이 일반적으로 사다리꼴입니다.

보통 경사면을 따라 거리를 측정하는 것이 편리하지만, 압력은 그림에서 보여 주는 것처럼 수직거리($h$)에 의해 결정됩니다.

 

cf)
잠긴 평면의 모양이 직사각형인 경우, 프리즘의 체적과 도심을 쉽게 구할 수 있으므로 압력프리즘을 이용하는 것이 편리합니다.(지금까지 위에서 나온 모든 잠긴 평면은 직사각형)

 

그러나 직사각형이 아닌 경우에는 체적과 도심을 구하기 위해서 일반적으로 적분이 필요합니다. 이 경우에는 잘 알려져 있는 유도된 방정식을 사용하는 것이 더 편리합니다. (아마 책 앞이나 뒤에 부록으로 있을 겁니다.)

---

잠긴 평면에 대한 대기압의 영향

잠긴 표면에 대한 대기압의 영향

우리는 지금까지 잠긴 표면에 대한 대기압의 영향은 아직 고려하지 않았습니다. (애초에 대부분의 문제에서 $0$으로 두기 때문이죠.)

대기압이 합력에 어떻게 영 향을 주는지 한번 알아봅시다.

지금까지 하던대로 왼쪽 그림과 같이 수직 벽면에 작용하는 압력분포를 다시 고려해 보면, 압력은 자유표면의 $0$에서 바닥의 $\gamma h$ 까지 변합니다.

자유표면에서의 압력을 $0$으로 놓았으므로 대기압을 기준으로 적용한 것이며, 유체에 의한 힘을 계산할 때 사용한 압력은 계기압력입니다. (자유표면에서의 압력이 $0$)

 

만약 대기압을 포함한다면 압력분포는 오른쪽 그림과 같게 됩니다.

이 경우 벽면의 한쪽에 작용하는 힘은 1. 정수압분포에 의한 $F_R$ 과 2. 대기압에 의한 $p_{\mathrm{atm}} A(A$ 는 벽면의 면적) 두 가지로 구성됩니다.

 

그러나 벽면의 한쪽에 대기압의 영향을 포함한다면, 같은 대기압 이 벽면의 바깥쪽에도 작용하고 있기 때문에(바깥 면이 대기에 노출되어 있다고 가정하면) 그림과 같이 크기는 같고 방향이 반대인 힘이 작용하게 됩니다. 따라서 평면에 작용하는 합력은 결국 평면과 접하고 있는 액체의 계기압력분포에 의한 것뿐이며, 대기압은 이 합력에 아무런 영향을 주지 않습니다.

 

cf) 물론 액체표면의 압력이 대기압과 다르다면(밀폐된 탱크의 경우처럼), 액체에 잠긴 면적 $A$ 에 작용하는 합력은 액체 표면의 계기압력을 $p_s$ 라 하면, 단순히 정수압에 의한 힘보다 그 크기가 $p_s A$ 만큼(바깥 면은 대기압에 노출되었다고 가정하면) 클 것입니다.

 

---

예제

 

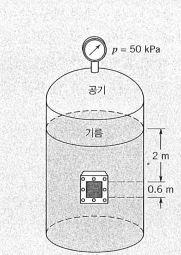
P1) 그림과 같이 기름 $(S G=0.90)$ 을 담고 있 는 가압탱크의 옆면에 한 변이 0.6 m 인 정사각형 평판이 볼 트로 고정되어 있다. 뱅크 위에 있는 압력계는 50 kPa 을 가라킨다. 밖은 대기압이다.

이 평판에 가해지는 합력의 크기와 방향을 구하라.

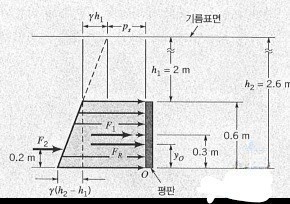
Hint : 아래 그림은 각각 정면에서의 사진, 압력프리즘의 사진이다.

P1, 1

P1, 2

Sol.

평판 안쪽 면의 압력분포가 그림에 그려져 있다.

평판의 주어진 한 점에 작용하는 압력은 그림과 같이 기름 표면 에서의 공기 압력 $p_s$ 와, 깊이에 따라 선형적으로 변하는 기름에 의한 압력으로 구성되어 있다.

단면적이 $A$ 인 평판에 작용하는 합력은 두 성분 $F_1$ 과 $F_2$ 에 의한 것이며, $F_1$ 과 $F_2$ 는 각각 사각형과 삼각형 압력분포에 의한 힘이다.

그러므로 분리해서 생각하면,
$$
\begin{aligned}
F_1= & \left(p_s+\gamma h_1\right) A \\
= & {\left[50 \times 10^3 \mathrm{~N} / \mathrm{m}^2\right.} \\
& \left.+(0.90)\left(9.81 \times 10^3 \mathrm{~N} / \mathrm{m}^3\right)(2 \mathrm{~m})\right]\left(0.36 \mathrm{~m}^2\right) \\
= & 24.4 \times 10^3 \mathrm{~N} \\
F_2= & \gamma\left(\frac{h_2-h_1}{2}\right) A \\
= & (0.90)\left(9.81 \times 10^3 \mathrm{~N} / \mathrm{m}^3\right)\left(\frac{0.6 \mathrm{~m}}{2}\right)\left(0.36 \mathrm{~m}^2\right) \\
= & 0.954 \times 10^3 \mathrm{~N}
\end{aligned}
$$

이다. 따라서 합력 $F_R$ 의 크기는

$$
F_R=F_1+F_2=25.4 \times 10^3 \mathrm{~N}=25.4 \mathrm{kN}
$$

이며 $F_R$ 이 작용하는 수직 위치는 $O$ 를 지나는 축에 대 하여 모멘트를 더하여 얻을 수 있다.
$$
F_R y_O=F_1(0.3 \mathrm{~m})+F_2(0.2 \mathrm{~m})
$$

또는
$$
\begin{aligned}
y_O & =\frac{\left(24.4 \times 10^3 \mathrm{~N}\right)(0.3 \mathrm{~m})+\left(0.954 \times 10^3 \mathrm{~N}\right)(0.2 \mathrm{~m})}{25.4 \times 10^3 \mathrm{~N}} \\
& =0.296 \mathrm{~m}
\end{aligned}
$$

이다. 따라서 합력은 평판의 수직 대칭축 선상에 있으며 평판 밑변에서 0.296 m 위에 작용한다.

---

수고하셨습니다.

다음 시간에는 곡면에 작용하는 정수력에 대해 알아보겠습니다.

 

이전 강의 보기

[유체역학 개념정리] 2.7 평면에 작용하는 정수력(hydrostatic force acting on a plane)

 

다음 강의 보기