[유체역학 개념정리] 2.7 평면에 작용하는 정수력(hydrostatic force acting on a plane)

목차

평면에 작용하는 정수력(hydrostatic force acting on a plane)

1. 평면에 작용하는 정수력(hydrostatic force acting on a plane) 예시 (개방 탱크)

2. 평면에 작용하는 정수력의 일반적 공식

3. 평면에 작용하는 정수력이 지나는 지점

4. 예제

오늘은 평면에 작용하는 정수력(hydrostatic force acting on a plane)에 대해 알아보고자 합니다. 유체역학 SI Version Munson 저 6판을 참고하여 작성하였습니다. (CENGAGE 출판사)'

 

이 단원은 정역학 (관성모멘트 및 1,2차모멘트) , 및 미분적분학(면적분) 등의 개념을 알아야 합니다.

따라서 다루지 않았다면 넘어가셔도 됩니다.

---

평면에 작용하는 정수력(hydrostatic force acting on a plane) 예시 (개방 탱크)

개방 탱크의 바닥에 작용하는 정수력

표면이 유체 속에 잠기면 유체에 의하여 표면에 힘이 작용합니다. 이 사실은 자명합니다.

앞에서도 계속해서 배웠지만, 정지된 유체의 경우, 전단응력이 없으므로 힘은 표면에 수직으로 작용합니다.

액체로 채워진 탱크의 바닥과 같은 수평면에 작용하는 합력의 크기는 단순히 $F_R=pA$ 이며, 여기서 $p$ 는 바닥에 작용하는 균일한 압력이고 $A$ 는 바닥의 면적이 됩니다. 위 그림처럼요!

바닥에서는 압력이 일정하고 균일하게 분포되어 있으므로 그림 $2.16a$ 와 같이 합력은 바닥면의 도심에 작용할 것입니다.

개방 탱크의 측면에 작용하는 정수력

이제 탱크 측면에서의 압력을 봅시다. 유체가 비압축성이면 압력은 위 그림과 같이 깊이에 따라 선형적으로 변할 것입니다.

cf) 아래 글을 참조하세요 ! 비압축성 유체, 즉 액체에 대해서는 높이차와 압력에 관한 매번 같은 공식이 사용됩니다.

[유체역학 개념정리] 2.3 정지된 유체 내의 압력 분포 (pressure distribution in a stationary fluid )

 

어쨌든 공식을 사용하면 위가 개방된 탱크에서는 $p=\gamma h$가 됩니다. (대기에서는 압력 0!)

그림처럼 대기압이 바닥의 양면에 작용할 경우, 바닥에 가해지는 합력은 단순히 탱크 안에 있는 액체 에 의한 것이다.

어쨌든, 탱크 측면의 압력분포는 그림 $2.16b$ 와 같이 균일하지 않습니다.

이 같은 경우에 대한 합력의 계산을 일반적인 경우를 사용해 해봅시다.

---

평면에 작용하는 정수력(hydrostatic force acting on a plane) 일반적 공식

평면에 작용하는 정수력

 

이 그림과 같이 잠긴 평면이 경사져 있는 일반적인 경우는 평면에 작용하는 합력을 구하는 것이 더 복잡합니다.

 

아래 가정을 따른다고 합시다:

유체의 표면이 대기에 노출된 것으로 가정합시다.

그림처럼 평면의 연장선이 액체의 자유표면(대기)과 교차하는 점을 $O$ 이라 하고 교차각을 $\theta$ 라 해봅시다.

$x-y$ 좌표계는 $O$ 이 원점이 되도록 정의하였습니다. 이때, $y=0$ ($x$ 축)이 자유표면(대기)라고 합시다.

그렇게 되면 위 그림처럼 그려질 수 있습니다.

 

여기서 액체와 접하고 있는 평면의 한쪽에 작용하는 합력의 방향과 위치, 그리고 크기를 구해봅시다.

임의의 깊이 $h$ 에 있는 그림 2.17의 미소 면적 $dA$ 에 작용하는 힘은 $dF=\gamma hdA$ 입니다.

($\gamma =\rho g$ 이고, 이때 $dV=hdA$ 이므로, 두 개를 곱하면 $dV\rho g=mg=F$ 이기 때문입니다!)

*밀도의 정의, 비중량의 정의, 힘의 정의를 생각해보세요 !!!!!

 

이 힘은 표면에 수직 방향으로 작용합니다.

따라서 이 미소 힘 $dF$들을 전체 표면에 걸쳐 더하면 합력의 크기를 얻을 수 있습니다.

 

식으로 나타내면, $h=y\sin \theta$ 이므로,
$$F_R={\int }_A\gamma hdA={\int }_A\gamma y\sin \theta dA$$
입니다. 면적분이 나와서 당황스러우실 수 있는데, 미분적분학 (2)에서 면적분을 다룹니다. (그냥 면에 있는 힘을 다 합쳐야 하니까 면에 대해 적분했다고 생각하세요!)

 

$\gamma$ 와 $\theta$ 가 일정하면
$$F_R=\gamma \sin \theta {\int }_{A}ydA$$

로 표현할 수 있습니다.

 

이때 식에 나타나는 적분은 $x$ 축에 대한 단면1차모멘트(first moment of area)이며
$${\int }_{A}ydA=y_{c}A$$
로 쓸 수 있습니다. (아래 식을 참조하세요)

여기서 $y_c$ 는 $x$ 축으로부터 측정한 면적 $A$ 의 도심의 $y$ 좌표입니다.

따라서 정리하면 다음과 같습니다.

Thm. 평면에 작용하는 정수력

$$F_R=\gamma A{y}_c\sin \theta$$
이때 $y_c$는 $y$축에 대한 도심
또는 더 간단히 표현하면
$$F_R=\gamma h_{c}A$$

$h_c$ 는 유체 표면에서 면적 도심까지의 수직거리

 

*도심과 모멘트는 정역학 강의에서 배울 수 있습니다. 도심을 배우지 않으셨다면 높은 확률로 이 차시를 학교에서 다루지 않을 것 같으니 한번 확인해 보세요.

cf) 특정 면에서 도심의 좌표 ($x-y$ 평면 가정)

$$y_c=\frac{{\int }_{A}ydA}{A}$$

$$x_c=\frac{{\int }_{A}xdA}{A}$$

 

위 식으로부터 합력의 크기는 각도 $\theta$ 에 관계가 없음을 알 수 있습니다.

즉, 유체의 비중량 $\gamma$, 전체 면적 $A$, 그리 고 자유표면에서 면적 도심까지 깊이 $h_c$에 의해서만 결정됩니다.

또한 합력 $F_R$ 을 얻기 위하여 더해진 모든 미소 힘들이 표면에 수직이므로, 합력 $F_R$ 도 표면에 수직입니다.

---

평면에 작용하는 정수력(hydrostatic force acting on a plane) 이 지나는 지점

평면에 작용하는 정수력(hydrostatic force acting on a plane) 이 지나는 지점

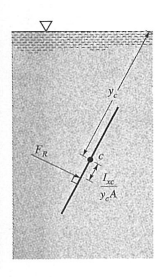
직관적으로는 합력이 평면의 도심을 지날 것 같으나 사실은 그렇지 않습니다.

합력의 $y$ 좌표를 $y_R$이라 합시다.

이는 $x$ 축을 중심으로 모멘트를 더하여 구할 수 있습니다.

즉 합력에 의한 모멘트는 압력힘 분포에 의한 모멘트와 같아야 하므로
$$F_R{y}_R={\int }_{A}ydF={\int }_A\gamma \sin \theta y^{2}dA$$
입니다.

이때 $F_R=\gamma A{y}_c\sin \theta$ 이므로

$$\gamma A{y}_c\sin \theta y_R={\int }_A\gamma \sin \theta y^{2}dA$$

로부터, y_R에 대해 표현하면,
$$y_R=\frac{{\int }_A{y}^{2}dA}{y_{c}A}$$
가 됩니다.

 

이때, 분자에 있는 적분은 평면의 연장선과 자유표면이 교차하여 형성되는 $x$ 축에 대한 단면2차모멘트(우리가 잘 아는 그 관성모멘트입니다. 정역학 참고) $I_x$ 입니다. 따라서 위 식을
$$y_R=\frac{I_x}{y_{c}A}$$

로 쓸 수도 있습니다. 아래 정의 참고하세요. 정역학에서도 나옵니다.

Def. 관성모멘트의 적분형 표현 - 정역학

$$I_x={\int }_A{y}^{2}dA$$

$$I_y={\int }_A{x}^{2}dA$$

Def. 평행축 정리 ($x$축에 대한) - 정역학

$$I_x=I_{xc}+A{y}_c^2$$

$I_x$ : 도심에서 $y$축 방향으로 $y_c$ 만큼 떨어진 지점에서의 관성모멘트

$I_{xc}$ : 도심에서의 관성모멘트
$A$ : 면적

$y_c$ : 도심에서 측정지점까지 $y$축 거리

위 내용을 사용하면,

$$y_R=\frac{I_x}{y_{c}A}=\frac{I_{xc}+A{y}_c^2}{y_{c}A}=\frac{I_{xc}}{y_{c}A}+y_c$$
이 됩니다.

Thm. 평면에 작용하는 정수력(hydrostatic force acting on a plane) 이 지나는 지점 - $y$좌표

$$y_R=\frac{I_{xc}}{y_{c}A}+y_c$$

 

이때, $I_{xc}/y_{c}A>0$ 이므로, 위 식에서 알 수 있듯이, 합력은 도심을 지나지 않고, 수평이 아넌 표면에서는 항상 도심의 아래에 있습니다.

---

합력의 $x$ 좌표 역시 앞과 같이 계산하면 됩니다. 다만 앞과 달리 $x_R$와 $x$를 곱해야 합니다.
$$F_R{x}_R={\int }_A\gamma \sin \theta xydA$$
으로부터, $x-R$에 대해 정리하면
$$x_R=\frac{{\int }_{A}xydA}{y_{c}A}=\frac{I_{xy}}{y_{c}A}$$

를 얻을 수 있습니다.

여기서 $I_{xy}$ 는 $x$ 와 $y$ 축에 대한 관성상승모멘트(product of inertia)입니다.

 

cf) 면적의 관성상승모멘트에 대한 평행축 정리는, 직각좌표계( $x-y$ 좌표계)에 대한 관성상승모멘트가 원래의 좌표계에 평행하면서 면적 도심을 통과하는 직각좌표계에 대한 관성상승모멘트와 면적과 면적도심의 $\mathrm{x},\mathrm{y}$ 좌표를 곱한 것을 더한 것과 같다는 것을 말합니다. 그러므로 $I_{xy}=I_{xyc}+A{x}_c{y}_c$ 입니다.

 

다시 평행축 정리를 사용하면 다음과 같이 쓸 수 있습니다.

Thm. 평면에 작용하는 정수력(hydrostatic force acting on a plane) 이 지나는 지점 - $y$좌표

$$x_R=\frac{I_{xyc}}{y_{c}A}+x_c$$

여기서 $I_{xyc}$ 는 $x-y$ 좌표계를 평행 이동하여 도심을 지나도록 만든 직교 좌표계에 관한 관성상승모멘트입니다.

 

잠긴 면적이 도심을 지나며 $x$ 축 또는 $y$ 축과 평행인 축에 대해 대칭이 면, $I_{xyc}$ 는 $0$이므로 합력은 $x=x_c$ 의 선상에 있습니다. (대부분의 대칭 도형)

위 식들 으로부터 $y_c$ 가 증가할수록 압력중심은 면적도심에 가까워짐을 알 수 있습니다.

또한 $y_c=h_d\sin \theta$ 이므로 잠긴 깊이 $h_c$ 가 커지거나, 또는 주어진 깊이에서 각도 $\theta$ 가 작아지도록 잠긴 면이 회전되면 거리 $y_c$ 가 증가하게 됩니다.

 

아래 그림을 참조하세요! 문제를 풀때 아주 유용합니다.

대표적인 도형들의 관성모멘트

---

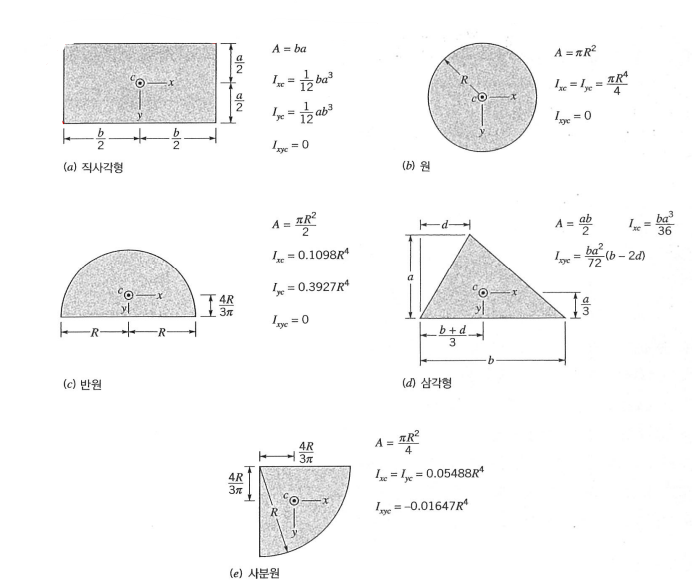
예제

이번에 이렇게 예제를 따로 모은 이유는,.. 난이도가 좀 있어서 그렇습니다.

천천히 풀어보시고 해설을 봐주세요.

 

P1 )그림과 같이 직경 4 m 인 원형 수문이 물 $(\gamma =9.80\mathrm{kN}/{\mathrm{m}}^3)$ 로 채워진 커다란 저수조의 경사진 벽에 설치되어 있다. 수문은 수평 방향의 직경을 따라 설치된 축에 의해 고정되어 있으며 축 위로 물의 깊이가 10 m 이다.

P1

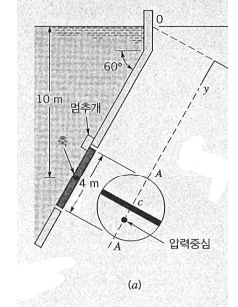
(1) 물에 의하여 수문에 가해지는 합력의 크기와 위치를 구하라.

(2) 수문을 열기 위해 축에 가해야 하는 모멘트를 구하라.

Sol.

(1) 물이 가하는 힘의 크기를 구하기 위해서는 식
$$F_R=\gamma h_{c}A$$

을 적용할 수 있으며, 수면으로부터 면적 도심까지 수직거리가 10 m 이므로 다음과 같이 된다.
$$\begin{array}{rl}{F}_R& =(9.80\times {10}^3\mathrm{N}/{\mathrm{m}}^3)(10\mathrm{m})\left(4\pi {\mathrm{m}}^2\right)\\ & =1230\times {10}^3\mathrm{N}=1.23\mathrm{MN}\end{array}$$
$F_R$ 의 작용점(압력중심)을 구하기 위하여 아까 구했던 식 2개를 사용한다.
$$x_R=\frac{I_{xyc}}{y_{c}A}+x_c{y}_R=\frac{I_{xc}}{y_{c}A}+y_c$$

그림의 좌표축에서는 수문이 대칭이고 압력중심은 직경 $A-A$ 위에 있어야 하므로, $x_R=0$ 이다.

$y_R$ 을 구하기 위해,
$$I_{xc}=\frac{\pi R^4}{4}$$

를 사용해야 한다.

이때 도심까지 거리 $y_c=\frac{10\mathrm{m}}{\sin {60}^{\circ }}$ 이다.

따라서
$$\begin{array}{rl}{y}_R=& \frac{(\pi /4)(2\mathrm{m}{)}^4}{(10\mathrm{m}/\sin {60}^{\circ })\left(4\pi {\mathrm{m}}^2\right)}+\frac{10\mathrm{m}}{\sin {60}^{\circ }}\\ & =0.0866\mathrm{m}+11.55\mathrm{m}=11.6\mathrm{m}\end{array}$$

이고 수문을 고정하는 축 아래로 압력중심까지의 거리는
$$y_R-y_c=0.0866\mathrm{m}$$

이다. 결론적으로 물이 수문에 가하는 힘의 크기는 1.23 MN 이고, 이 힘은 수문의 회전축으로부터 0.0866 m 아래의 점에( 지름 $A-A$ 를 따라) 작용한다. 힘은 수문의 면에 직각이다.

 

(2) 수문을 여는 데 필요한 모멘트는

P1, (2)

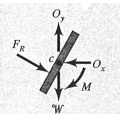
위 그림을 참고하여 구할 수 있다.

이 그림에서 $W$ 는 수문의 무게이고 $O_x$ 와 $O_y$ 는 수문 위의 축에 작용하는 수평한 수직 반력이다.

축에 대하여 모멘트를 더하면
$$\sum M_c=0$$
이므로
$$\begin{array}{rl}M& =F_R(y_R-y_c)\\ & =(1230\times {10}^3\mathrm{N})(0.0866\mathrm{m})\\ & =1.07\times {10}^5\mathrm{N}\cdot \mathrm{m}\end{array}$$

이다.

P2) 그림과 같이 수족관에 바닷물 $(\gamma =10.1$ $\mathrm{kN}/{\mathrm{m}}^3$ )이 0.3 m 깊이까지 채워져 있다. 수족관 한쪽 구석에 파손된 부분을 수리하기 위해 그림과 같은 삼각형 모양의 판을 새것으로 교환하였다.

(a) 바닷물에 의해 이 삼각형 면에 작용하는 힘의 크기를 구하라.
(b) 힘의 위치를 구하라.

아래 그림을 참조할 것.

P2

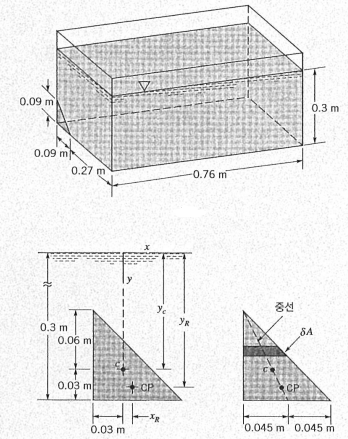
Sol.

(a) 이 문제를 푸는 데 필요한 여러 가지 길이가 그림에 표시되어 있다.

관심의 대상인 표면이 수직면 상에 있으므로 $y_c=h_c=0.27\mathrm{m}$ 이고,

식 2.18 로부터 합력의 크기는
$$\begin{array}{rl}{F}_R& =\gamma h_{c}A\\ & =\left(10.1\mathrm{kN}/{\mathrm{m}}^3\right)(0.27\mathrm{m})((0.09\mathrm{m}{)}^2/2)=11\mathrm{N}\text{ (답) }\end{array}$$
이다.

(b) 압력중심(CP)의 $y$ 좌표는 위에서 구한 식으로부터
$$y_R=\frac{I_{xc}}{y_{c}A}+y_c$$
이고, 잘 알려져 있는 관성모멘트 식으로부터
$$I_{xc}=\frac{(0.09\mathrm{m})(0.09\mathrm{m}{)}^3}{36}=\frac{6.6\times {10}^{-5}}{36}{\mathrm{m}}^4$$
이므로 다음과 같다.
$$\begin{array}{rl}{y}_R& =\frac{6.6\times {10}^{-5}/36{\mathrm{m}}^4}{(0.27\mathrm{m})\left((8.1\times {10}^{-3}/2){\mathrm{m}}^2\right)}+0.27\mathrm{m}\\ & =0.0017\mathrm{m}+0.27\mathrm{m}=0.272\mathrm{m}\end{array}$$
마찬가지로 $x$ 좌표는 정의된 식으로부터
$$x_R=\frac{I_{xyc}}{y_{c}A}+x_c$$

이고, 잘 알려져 있는 관성모멘트 식으로부터
$$I_{xyc}=\frac{(0.09\mathrm{m})(0.09\mathrm{m}{)}^2(0.09\mathrm{m})}{72}=\frac{6.6\times {10}^{-5}}{72}{\mathrm{m}}^4$$
이므로
$$x_R=\frac{(6.6\times {10}^{-5}/72){\mathrm{m}}^4}{(0.27\mathrm{m})\left((8.1\times {10}^{-3}/2){\mathrm{m}}^2\right)}+0=8.38\times {10}^{-4}\mathrm{m}$$

이다.

---

수고하셨습니다.

다음 시간에는 압력프리즘에 대해 알아보겠습니다.

 

이전 강의 보기

[유체역학 개념정리] 2.6 액주계(manometer)

 

다음 강의 보기

[유체역학 개념정리] 2.8 압력프리즘(pressure prism)