목차
1. 점성계수
점성계수 유도 (1) - 고체에서의 거동
점성계수 유도 (2) - 유체에서의 거동, 전제 조건(점착조건, no slip condition)
점성계수 유도 (3) - 점성계수의 유도
점성계수의 종류(Newton 유체, 비 Newton 유체)
점성계수의 특성과 온도에 따른 영향(Sutherland 식)
2. 동점성계수
동점성계수
시작하기 전에..
유체역학을 처음 배우는 분들, 유체역학을 다시 보고 싶으신 분들, 혹은 유체역학에 대해 알고 싶어서 오신 분들 환영합니다!
저는 대학에 다니고 있는 대학생으로, 제가 공부했던 여러 학문 분야들의 내용을 정리하여 새로이 배우는 분들에게 더 쉬운 이해를 주고자 게시글을 작성하게 되었습니다!
대학과목 특성상 자료도 찾기 쉽지 않고 어렵기에 다양한 예시와 그림들, 그리고 문제들과 설명을 통해 많은 내용을 전달하고자 합니다.
오늘은 점성계수(점도; Viscosity)에 대해 알아보고자 합니다.
유체역학 SI Version Munson 저 6판을 참고하여 작성하였습니다. (CENGAGE 출판사)
점성계수
점성계수 유도 (1) - 고체에서의 거동
밀도와 비중량은 유체를 대략적으로 구분할 수 있습니다. 그런데 유동의 양상이 워낙에 다양하고 복잡하다 보니 이들만으로 유체를 구분하기엔 어렵습니다. 따라서 유체의 거동 특성을 조금 더 나타낼 수 있는 것이 바로 점성계수입니다.
점성계수를 유도하기 위해서는 먼저 고체에서의 전단력에 따른 거동을 살펴봐야 합니다.
아래와 같은 상황이 주어졌다고 합시다.

가운데에 있는 물질이 강철이라고 합시다.(고체)
그림과 같이 힘 $P$가 가해진다면, 미소 거리 $\delta a$ 만큼 고체가 이동할 것입니다.
또한 수직선 $A B$ 는 작은 각 $\delta \beta$ 만큼 회전하여 새로운 위치 $A B^{\prime}$ 으로 이동합니다.
(물론 첫 강의에서 배웠듯 고체의 정의에 의해, 약간의 변형 후에는 더 이상 이동하지 않습니다.)

정역학에서도 나오는 내용이지만 변형이 발생하면 그에 맞게 전단력이 발생합니다.
가해진 힘 $P$ 에 저항하기 위해서는 경계면에 전단응력 $\tau$ 이 발생하게 될 것이고,
고정평판의 옆면적을 $A$ 라 할 때, 힘의 평형을 이루기 위해 $P=\tau A$ 의 관계가 성립합니다.
또한 고체에서 작은 각도의 변위 $\delta \beta$ (전단 변형)은 전단 응력 ( $\tau$ )에 비례합니다.
(위의 내용은 고체를 다루는 정역학의 내용이므로 식의 전개 방식만 이해하시면 됩니다.)
그럼 왜 고체일 때의 상황을 따져보았는가? 유체일 때는 고체와 달리 지속적인 변화가 있기 때문에 식을 세울 때의 관점이 완전히 다르기 때문입니다.
점성계수 유도 (2) - 유체에서의 거동, 전제 조건(점착조건, no slip condition)
초기의 큰 변동을 제외하고, 유체는 결국 변형을 받으면 일정한 속도로 계속 운동할 것입니다.

고체와 똑같이 힘 $P$가 가해졌다고 합시다. 일정 시간이 지나면 속도가 $U$가 될 것입니다.
(유체는 외력/전단력을 가했을 때 변형이 지속적으로 일어난다고 1.1에서 배웠습니다!)
그런데 식을 더 세우려면 다음 한 가지 가정이 필요합니다. 바로 점착조건입니다.
유체역학에서 점착조건(no slip condition)은 유체가 고체의 경계면에 붙는 현상을 말합니다.
즉, 위의 그림에서 윗부분의 유체는 힘 $P$를 받아 속도 $U$를 지니고 움직입니다. 그러나 아랫부분의 유체는 정지해 있습니다. 왜 그럴까요?
아랫부분의 유체가 고정 평판에 점착되어 있기 때문입니다.
그래서 윗부분에 힘을 가했을 때 위쪽 유체만 움직이고 아래쪽 유체는 영향을 받지 않는 겁니다.
모든 유체는 이 점착조건을 만족합니다. 절대 잊으시면 안 됩니다!!
그럼 가운데 부분은 어떨까요?
가운데에 있는 유체는 그림의 경우에는 선형 변화를 띄게 됩니다.(문제에 따라 아닐 수도 있습니다.)
파란색으로 표기된 삼각형에 집중해 봅시다.
높이에 따른 속도 함수 $u=u(y)$를 정의해 봅시다. 이때 속도와 높이는 선형 관계를 띄고 있습니다.
기울기는, 파란색 삼각형에서 생각하면 $\frac {U}{b}$가 됩니다. 따라서, 속도 함수 $u$는,
$$u(y)=\frac {Uy}{b}$$입니다.
미분적분학에서 배울 수 있는 그래디언트를 사용하여, 속도 gradient의 y성분을 계산할 수 있습니다.
이 유체는 선형 거동을 하므로, 속도 구배(velocity gradient)는,
$$ \frac {du}{dy}=\frac {U}{b} $$
입니다. (그냥 위 식을 미분한 것입니다 ~) 이를 활용하여 점성계수를 정의해 봅시다!
점성계수 유도 (3) - 점성계수의 유도

미소 시간 $\delta t$ 동안에 수직선 $A B$ 는 작은 각도 $\delta \beta$ 만큼 회전하게 되므로
$$
\tan \delta \beta \approx \delta \beta=\frac {\delta a}{b}
$$
가 됩니다. (주어진 그림의 오른쪽 삼각형을 잘 보세요!)
속도의 정의에 의해 $\delta a=U \delta t$ 이므로
$$
\delta \beta=\frac {U \delta t}{b}
$$
가 됩니다.
이때 $\delta \beta$ 가 고체에서와 달리 위 식에서 볼 수 있듯 시간의 함수입니다.( $\delta t $)
고체에서는 힘 $P$에 대해 식을 세웠으나 유체에서는 힘의 성분도 물론 들어가 있지만($U$ 자체가 힘 $P$ 에 의해 발생한 것) 시간의 성분도 들어가 있기에 시간 변수 $t$를 고려하는 것이 적절할 것으로 보입니다.
따라서 고체의 경우에서와 같이 전단응력 $\tau$ 을 $\delta \beta$ 와 연관 지으려는 것은 논리적 오류가 있습니다.
그 대신 $\delta \beta$ 의 변화율을 고려해서 전단변형률(rate of shearing strain) $\dot {\gamma}$ 를
$$
\dot {\gamma}=\lim _{\delta t \rightarrow 0} \frac {\delta \beta}{\delta t}
$$
와 같이 정의합니다.(미분의 정의를 그대로 이용하여 전단력의 1차 시간에 대한 미분 형태를 계산한 것입니다.)
이때 위에서 구한 식 $ \delta \beta=\frac {U \delta t}{b} $를 대입하면
$$
\dot {\gamma}= \lim_{ \delta t\to 0}\frac {\delta \beta }{\delta t}=\lim_{ \delta t\to 0}\frac{(\frac{U \delta t}{b})}{\delta t}=\frac{U}{b}\lim_{ \delta t\to 0}\frac{\delta t}{\delta t}=\frac{U}{b}=\frac{du}{dy} $$
와 같이 됩니다.
($ \lim_{ \delta t\to 0}\frac{\delta t}{\delta t}=1$ 인 것은 자명합니다!)
(전 소단원에서 구한 속도 그래디언트
$\frac{du}{dy}=\frac{U}{b}$ 를 통해 마지막까지 계산해 줍니다!)
이제 거의 다 왔습니다. 이번 실험에서 $P$ 를 증가시키면 전단응력 $\tau$ 이 증가 $(\tau=P / A$ 이므로) 하는 것은 당연합니다! 힘의 평형 때문이죠. 이때 전단변형률도 비례적으로 증가됩니다.(이 내용은 자명한 사실로 받아들이면 됩니다! 더 많은 내용을 보고 싶으시면 정역학을 보시면 됩니다!) 즉
$$
\tau \propto \dot {\gamma}
$$
이고, 최종 결론은
$$
\tau \propto \frac {d u}{d y}
$$
입니다.
이 결과는 물이나 기름, 휘발유, 공기 등과 같은 일반적인 유체에서, 전단응력과 전단 변형률(속도 그래디언트)이다음과 같은 관계를 가지는 것을 알 수 있습니다! 이때 비례상수 $\mu$가 점성 계수입니다.
$$
\tau=\mu \frac {d u}{d y}
$$
식에서 유도되듯이,
점성계수의 단위는 $\mathrm {N} \cdot \mathrm {s} / \mathrm {m}^2$입니다.
또한 FLT 단위계를 사용하면 점성계수는 $F L T^{-2}$로 표현됩니다.
점성계수의 종류(Newton 유체, 비 Newton 유체)
점성계수 $\mu$ 는 절대점성계수(absolute viscosity) 또는 역학적 점성계수(dynamic viscosity)로 불리기도 합니다. (모두 같은 말입니다.)
점성계수의 특징에 따라 유체를 두 가지로 나눌 수 있습니다.
Newton 유체 : 전단응력과 전단변형률이 선형적 관계를 띄는 유체, 즉 $ \tau \propto \dot {\gamma} $가 선형적 비례관계를 가지는 유체를 말합니다.
비 Newton 유체 : 전단응력과 전단변형률이 비선형적 관계를 띄는 유체를 말합니다.
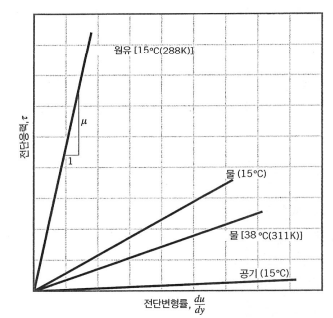
대부분의 유체는 Newton 유체입니다. 여러 가지 Newton 유체들의 전단응력과 전단변형률 직선은 위 사진과 같습니다.
물, 기름, 공기 등 대부분의 유체가 Newton 유체에 포함됩니다.
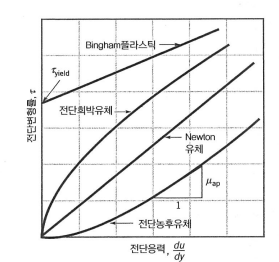
그러나 몇몇 유체는 비 Newton 유체입니다...
*그림에 오류가 있습니다. x축이 전단 변형률로 바뀌어야 합니다. y축이 전단 응력으로 바뀌어야 합니다.
주어진 그림에서 $\mu_{ap}$는 겉보기점성계수(apparent viscosity)로 임의의 곡선에서 두 점 사이의 기울기를 의미합니다. (수학에서 곡선의 순간변화율과 같습니다.) 이 겉보기점성계수를 통해 비Newton 유체의 종류가 나누어집니다.
비Newton 유체는 또 3종류로 나누어집니다. (상당히 복잡합니다;;)
전단 희박 유체(shear thinning fluid): 전단변형률이 증가함에 따라 겉보기점성계수가 감소하는 유체입니다. 즉, 전단이 더 될수록 점성이 작아집니다. 현탁액이나 콜로이드, 고분자용액 이 여기에 해당됩니다.
전단 농후 유체(shear thickening fluid): 전단변형률이 증가함에 따라 겉보기점성계수가 증가하는 유체입니다. 즉, 전단이 더 될수록 점성이 커집니다. 물과 녹말이나 물과 모래의 혼합물 등이 있습니다. (물과 모래의 혼합물을 빨리 제거하려고 할 때 더 어려운 이유가 이것 때문입니다.)
Bingham플라스틱(유체도 고체도 아닙니다!):
이 물질은 영이 아닌 전단응력 즉, 항복응력 $\tau_{\text {yield }}$까지는 그 형태를 거의 유지할 수 있습니다. (따라서 유체로 보긴 어렵습니다.)
그런데 항복응력을 초과하게 되면 유체처럼 흐릅니다.(따라서 고체로 보기도 어렵습니다).
치약과 마요네즈가 Bingham플라스틱의 대표적인 예입니다.
예제를 통해 점성계수를 활용해 봅시다!
Ex 1)
두 개의 평판 사이를 흐르는 Newton 유체의 속도 분포 $u$가
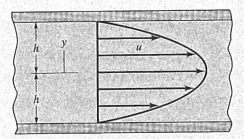
$$u=\frac {3 V}{2}\left [1-\left(\frac {y}{h}\right)^2\right]$$
라고 하자.
평균 속도 $V=0.6 \mathrm {~m} / \mathrm {s}$,
중간 부분에서부터 윗부분까지의 높이 $h=5 \mathrm {~mm}$라고 하자.
유체의 점성계수는 $2 \mathrm {~N} \cdot \mathrm {s} / \mathrm {m}^2$이다.
(1) 아래 벽면의 전단응력을 구하시오.
(2) 중앙 부분에서의 전단응력을 구하시오.
Sol.
위에서 구한 전단 응력 공식은 다음과 같습니다.
$$
\tau=\mu \frac {d u}{d y}
$$
따라서 속도분포 $u=u(y)$ 를 알면 속도의 $y$에 대한 미분 $d u / d y$ 를 계산함으로써 모든 점에서의 전단응력을 알 수 있습니다. 따라서 먼저 $u$를 $y$에 대해 미분합시다.
$$
\frac {d u}{d y}=\frac {d}{d y}(\frac{3 V}{2}\left[1-\left(\frac{y}{h}\right)^2\right])=-\frac{3 V y}{h^2}
$$
이제 모든 구간 $y=[-h, h]$에서의 전단응력을 구할 수 있습니다!
(1) 아래 벽면에서는 $y=-h$이므로
$$
\frac{d u}{d y}=\frac {3 V}{h}
$$
이고, 따라서 전단응력은 주어진 수치를 대입하면 됩니다. (미터 단위로 환산하는 걸 잊지 마세요! 다른 단위는 다 맞습니다. 유체역학에서는 단위가 정말 중요합니다!)
$$
\begin {aligned}
& \tau_{\substack {\text { bottom } \\
\text { wall }}}=\mu \frac {d u}{d y} =\mu\left(\frac {3 V}{h}\right)=\frac {\left(2 \mathrm {~N}. \mathrm {s} / \mathrm {m}^2\right)(3)(0.6 \mathrm {~m} / \mathrm{s})}{(5 \mathrm{~mm})(1 \mathrm{~m} / 1000 \mathrm {~mm})} \\
& =720 \mathrm {~N} / \mathrm {m}^2 \\
&
\end {aligned}
$$
(2) 중간 벽면에서는 $y=0$입니다.
($y$가 왜 아랫부분에서 시작하지 않을까요? 속도 식과 그림의 포물선을 비교하면 최고점이 $y=0$인 부분에서 발생하기 때문입니다.)
따라서 $y=0$을 대입하면,
$$\frac{du}{dy}=0$$
이므로,
$$\tau_{\text {midplane }}=0$$
입니다.
점성계수의 특성과 온도에 따른 영향(Sutherland 식)
점성계수는 온도에 따라서도 매우 예민하게 변합니다.
예를 들어 물은 1도의 변화에도 40% 이상의 점성계수 변화가 일어납니다.
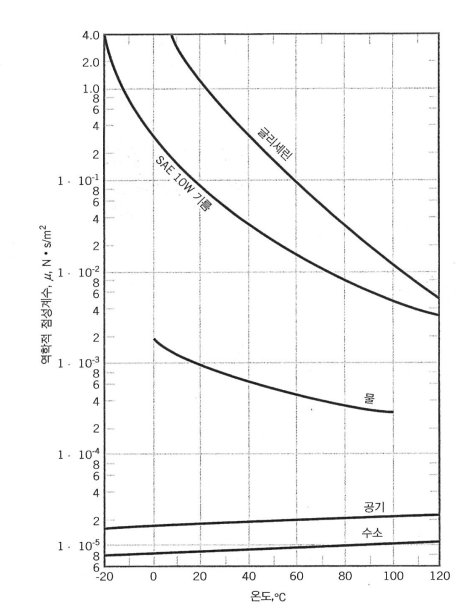
그림으로부터 알 수 있듯이,
기체는 온도와 점성계수가 비례하고,
액체는 온도와 점성계수가 반비례합니다.
왜 그럴까요? 일반화학 시간에 배웠던 걸 다시 떠올려 봅시다.
액체의 분자들은 그들 사이의 강한 응집력 때문에 조밀하게 분포되어 있습니다. 온도가 증가함에 따라 분자 간의 응집력은 감소하고, 결과적으로 운동에 저항하는 힘도 감소합니다. 점성계수는 이 저항력과 비례하므로, 온도가 증가함에 따라 점성계수는 감소합니다.
그러나 기체의 경우, 분자들은 서로 멀리 떨어져 있고, 그들 사이의 결합력은 무시할 수 있을 정도로 매우 작습니다. 평균속도가 작은 영역에서 평균속도가 큰 영역으로(또는 그 반대로), 기체 분자들이 무작위적인 운동을 하여 이동하게 되면 실질적인 운동량의 교환이 일어나게 됩니다. 즉 운동을 더 많이 한다는 것입니다. 이는 유체 층 사이의 상대운동에 저항력을 늘리는 결과를 낳습니다. 따라서 기체 온도가 올라감에 따라 분자들의 무작위적인 운동은 더 활발해지고, 이것은 점성계수의 증가로 나타납니다.
이를 수식적으로 표현할 수도 있습니다.
Sutherland 식은, 기체에서 점성계수와 온도 간의 관계를 보여주는 식을 근사적으로 만들었습니다. 식은 다음과 같습니다.
$$
\mu=\frac {C T^{3 / 2}}{T+S}
$$
입니다. ($T$는 절대 온도, $\mu$는 점성 계수)
미지수가 $C$와 $S$ 두 개이므로, 두 온도에서의 점성계수 ($T$ 2개, $\mu$ 2개)를 알면 연립방정식을 통해 미지수 2개를 모두 구할 수 있겠네요.
Andrade 식은, 액체에서 점성계수와 온도 간의 관계를 보여주는 식을 근사적으로 만들었습니다. 식은 다음과 같습니다.
$$
\mu=D e^{B / T}
$$
입니다. ($T$는 절대 온도, $\mu$는 점성 계수)
앞과 마찬가지로 미지수가 $D$와 $B$ 두 개이므로, 두 온도에서의 점성계수 ($T$ 2개, $\mu$ 2개)를 알면 연립방정식을 통해 미지수 2개를 모두 구할 수 있겠네요.
동점성계수(kinematic viscosity)
동점성계수
점성계수와 밀도를 함께 나타내어서 표현하고자 만든 것이 바로 동점성계수입니다.
동점성계수(kinematic viscosity)란, 유체에서 점성계수를 밀도로 나눈 값입니다.
아래와 같은 식을 가집니다.
$$
\nu=\frac {\mu}{\rho}
$$
이때 동점성계수는 $v(\mathrm {nu})$ 를 사용합니다.
동점성계수의 차원은 FLT나 MLT에 관계없이 $L^2 / T$입니다.
동점성계수의 단위는 SI단위계로 $\mathrm {m}^2 / \mathrm {s}$입니다!
동점성계수는 점성계수보다는 덜 등장하지만 가끔 사용되니 꼭 알아두도록 합시다!
읽어주셔서 감사합니다!
다음 시간에는 1단원에서 조금 어려운 부분인 체적계수 부분과 음속을 다루려고 합니다.
이전 강의 보기
[유체역학 개념정리] 1.2 유체의 밀도, 비중량, 비중 , 이상기체의 법칙(density, specific weight, specific
목차1. 유체의 질량밀도비중량비중2. 이상기체의 법칙이상기체의 법칙절대압력, 계기압력시작하기 전에..유체역학을 처음 배우는 분들, 유체역학을 다시 보고 싶으신 분들, 혹은 유체역학에 대
azale.tistory.com
다음 강의 보기
[유체역학 개념정리] 1.4 유체의 압축성(등엔트로피 압축), 체적계수, 음속(incompressible, bulk modulus,
목차1. 유체의 압축성(compressibility)체적계수와 비압축성등온과정과 등엔트로피과정에서의 체적계수2. 음속(Speed of sound)음속 시작하기 전에..유체역학을 처음 배우는 분들, 유체역학을 다시 보고
azale.tistory.com



