목차
1. 증기압 (vapor pressure)
증기압 (vapor pressure)
비등과 공동현상 (Boiling, cavitation)
2. 표면 장력(surface tension)
표면 장력(surface tension)
모세관 현상(Capillary action)
시작하기 전에..
유체역학을 처음 배우는 분들, 유체역학을 다시 보고 싶으신 분들, 혹은 유체역학에 대해 알고 싶어서 오신 분들 환영합니다!
저는 대학에 다니고 있는 대학생으로, 제가 공부했던 여러 학문 분야들의 내용을 정리하여 새로이 배우는 분들에게 더 쉬운 이해를 주고자 게시글을 작성하게 되었습니다!
대학과목 특성상 자료도 찾기 쉽지 않고 어렵기에 저도 공부하는데 많이 힘들었었는데, 다양한 예시와 그림들, 그리고 문제들과 설명을 통해 많은 내용을 전달하고자 합니다.
오늘은 증기압, 표면 장력, 모세관 현상(vapor pressure, surface tension, Capillary action)에 대해 알아보고자 합니다. 유체역학 SI Version Munson 저 6판을 참고하여 작성하였습니다. (CENGAGE 출판사)
증기압 (vapor pressure)
증기압 (vapor pressure)
증발이란 무엇일까요? 화학 시간에 많이 들어본 말이죠.
증발은 표면의 액체분자들의 운동량이 분자 간의 결합력을 극복할 수 있을 때(즉, 결합을 빠져 나올 수 있는 힘이 더 셀 때) 대기 중으로 분자가 나가는 현상을 말합니다.
밀폐된 용기 속에 부분적으로 액체가 채워져 있을 때, 용기 속의 나머지 공간에서 공기를 제거한다면(즉, 액체만 남겨두면) 그 공간에는 액체 표면으로부터 탈출한 증기에 의해 압력이 형성됩니다.
증기압(vapor pressure) $p_v$ 이란, 액체 표면에서 탈출하는 분자의 수와 액체 표면에 부딪혀 달라 붙는 분자의 수가 같아지는 평형상태에 도달했을 때(증기가 포화되었을 때) 증기 가 액체 표면에 작용하는 압력을 말합니다.
위 그림을 보면, 액체로 완전히 채워진 용기의 한쪽 면을 용기에 공기를 넣지 않으면서 피스톤을 당긴다고 해봅시다.
그렇게 되면 액체와 당기는 면 사이에는 증기압과 같은 압력의 증기로 채워지게 됩니다.
증기압의 발생은 분자의 운동과 밀접한 관계를 가집니다. 그래서 액체의 증기압은 온도에 의존하는 경향이 있습니다.
비등과 공동현상 (Boiling, cavitation)
비등(Boiling)이란, 액체 내부에서 증기의 기포가 형성되는 과정을 말합니다.
비등이 일어나는 조건은 액체의 절대압력이 증기압에 도달할 때 일어납니다.
우리가 정말 익히 잘 알고 있듯이, 표준대기압에서의 물은 온도 가 $100^{\circ} \mathrm{C}(373 \mathrm{~K})$ 일 때 비등합니다. 즉, 온도가 $100^{\circ} \mathrm{C}(373 \mathrm{~K})$ 인 물의 증기압은 $101.3 \mathrm{kPa}(\mathrm{abs})$ 이라는 것이죠. 끓는점이 100도라는 걸 모두 다 알고 계실 겁니다.
그러나 예를 들어, 기압이 $30 \mathrm{kPa}(\mathrm{abs})$ 인 해발 $9,000 \mathrm{~m}$ 의 높은 고도(Everest 산의 높이 정도)에서 물을 비등시키려고 한다면, 물이 약 $69^{\circ} \mathrm{C}(294 \mathrm{~K})$ 가 될 때부터 비등하기 시작합니다! 이 온도에서 물의 증기압은 $30 \mathrm{kPa}(\mathrm{abs})$ 가 됩니다. 고도에 따라 증기압이 달라지는 것이죠!
나중에 배우겠지만 대기의 고도에 따라서 압력이 달라집니다. (2절에서 다룹니다.)
위 그림을 참조하세요!'
증기압과 비등에 관심을 가지는 이유는 액체가 흐를 때 압력이 매우 낮아지는 경우가 있는데 이때 비등이 일어날 수 있기 때문입니다.(액체가 기체로 변한다는 소리입니다)
예를 들어, 불규칙적인 모양을 지닌 펌프나 수로 내의 유동에서 이러한 현상이 일어날 수 있습니다.
흐르는 액체 속에서 증기 기포가 발생하면, 기포는 결국 압력이 높은 영역으로 휩쓸려가게 되고 이는 갑작스러운 기포의 와해(공동현상, cavitation)으로 이어집니다. 이는 실제로 구조의 손상을 가져올 수 있을 정도의 강력한 영향을 일으킵니다.
액체가 흐를 때 증기 기포의 발생과 이에 따르는 와해를 공동현상(cavitation)이라고 합니다. 이는 3장에서 다룹니다!
표면 장력(surface tension)
표면 장력(surface tension)
만일 액체와 기체 또는 서로 섞이지 않는 두 액체를 같이 놓으면 사이의 경계면을 따라 힘이 발생합니다.
이것은 마치 경계면에 "껍질"이나 "막"이 존재하는 것처럼 보입니다.
(어쨌든 경계가 있으니 구분이 가는 거겠죠?)
물론 막이 실제로 존재하는 것은 아닙니다.
그렇지만 표면 장력이라는 개념을 이용하면 흔히 관찰되는 현상들을 설명하기 쉬워집니다.
예를 들어, 어떤 물체(나뭇잎이나 사람 등등..)들은 물 위에 뜨는데,
이 현상을 가상적인 막에 발생한 장력이 바늘을 떠받치고 있기 때문이라고 생각할 수 있습니다.
이렇게 표면 장력을 새로이 정의할 수 있습니다.
이러한 여러 가지의 표면 현상은 액체 표면의 분자들에 작용하는 응집력의 불균형에서 발생합니다. 액체 표면에 있는 분자가 다른 분자들에 의해 받는 힘들의 합은 그 방향이 액체 내부를 향하게 됩니다.
액체 표면을 따라서 일어나는 이러한 힘의 불균형은 겉으로 보기에는 마치 가상적인 막이 생긴 것처럼 보이게 됩니다.
즉, 액체 표면 위에는 그 면 위 에 있는 가상적인 임의의 모든 선을 따라서 인장력이 작용하고 있다고 볼 수 있습니다.
표면장력 (surface tension)이란, 액체 표면 위에서 임의의 선을 따라 작용하는 분자 간의 인력의 단위길이당 강도를 말합니다.
표면 장력은 그리스 문자 $\sigma(\mathrm{sigma})$ 로 표시합니다.
표면장력은 액체의 성질이 고, 온도 및 액체의 계면에서 접촉하고 있는 유체의 종류에 따라 달라집니다.
표면장력의 차원 은 $F L^{-1}$ 이고 SI 단위계로는 $\mathrm{N} / \mathrm{m}$ 입니다.
cf) 표면장력은 액체 온도가 높아질수록 작아집니다.
액체 방울에서의 표면 장력
표면장력은 어떻게 보면 상당히 추상적이고 다루기 힘듭니다. 계산 과정도 상당히 복잡합니다.
먼저 액체 방울에서 표면장력을 살펴봅시다.
액체가 구체라고 가정합시다.
그리고, 반으로 자릅시다. 그렇게 되면 그림에서 표면에서의 힘(표면장력)은,
원주 길이$2 \pi R$ $\times$ 표면 장력 $\sigma$ 로 계산하면,
$$2 \pi R \sigma$$
가 됩니다.
이때 액체 내부압력 $p_i$ 와 외부압력 $p_e$ 의 차이인 $\Delta p$ 가 존재합니다.
압력이 원형단면 $\pi R^2$ 에 작용하는 힘과 같아야 합니다. (힘의 평형!)
압력과 면적의 곱은 힘이었죠! 따라서 $F=\Delta p \pi R^2$으로부터,
$$
2 \pi R \sigma=\Delta p \pi R^2
$$
가 됩니다.
이를 적절히 정리하면 압력 차이는
$$
\Delta p=p_i-p_e=\frac{2 \sigma}{R}
$$와 같습니다!
이 결과는 기체 내부 압력이 외부 압력 보다 크다는 것을 알려줍니다!
$ \Delta p>0 $ 이기 때문이죠!
모세관 현상(Capillary action)
표면장력 관련 문제는 거의 모세관과 관련된 문제라도 봐도 무방할 정도로 이번에 배우는 공식은 중요합니다!
꼭 외우고 계셔야 합니다. 대학교에서 서술을 요구하는 경우가 많으므로 가능하면 유도과정까지 알아둡시다.
표면장력에 관한 일반적인 현상 중에 모세관 속의 액체가 모세관을 따라 올라가거나 내려가는 현상이 있습니다. 위 그림에서처럼, 끝이 개방된 작은 튜브를 물속에 넣으면, 튜브 속의 수면이 튜브 밖의 수면보다 높아집니다.
이 현상이 발생하는 이유는, 튜브 벽과 액체 사이의 인력(부착력)이 액체 분자들 사이의 상호인력(응집력)을 극복할 수 있을 정도로 강해서, 액체가 튜브 벽을 따라 끌어올려지기 때문입니다.
액체기둥의 높이 $h$ 는 표면장력 $\sigma$ 튜브의 반경 $R$ 액체의 비중량 $\gamma$ 그리고 액체와 튜브 사이의 접촉각(contact angle) $\theta$ 에 의해 결정됩니다.
두 번째 그림의 자유물체도에서
표면장력에 의한 수직 방향의 힘은 $2 \pi R \sigma \cos \theta$ (위 단원에서 힘이 $2 \pi R \sigma$ 였는데, 각도가 수평이 아니기 때문에 코사인 값을 곱해야 합니다!)
또한 액체기둥의 무게는 부피와 비중량 (Specific Weight)를 곱한 값인 $\gamma \pi R^2 h$ 입니다.
이때 두 힘이 평행을 이루어야 하므로,
$$
\gamma \pi R^2 h=2 \pi R \sigma \cos \theta
$$
입니다.
높이에 대해 정리하면,
$$
h=\frac{2 \sigma \cos \theta}{\gamma R}
$$
가 됩니다. 위 두개 공식은 꼭 알아두세요!
접촉각은 어떻게 결정될까요? 접촉각은 액체와 튜브 접촉면에 따라 결정됩니다.
즉, 종류, 상황에 따라 모두 다 다르다는 소리입니다.
물이 깨끗한 유리와 접촉하고 있는 경우가 접촉각이 $\theta \approx 0^{\circ}$ 인 경우입니다.
또한 위 식으로부터 높이는 튜브의 반경에 반비례하고 있음이 분명합니다.
즉 같은 상황일 경우 높이 $h$와 반경 $R$은 반비례합니다.
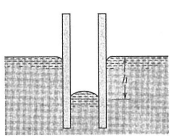
액체분자와 고체 벽 사이의 부착력이 액체분자들 사이의 응집력에 비해 약할 경우에는 (부착력<응집력)
튜브 속의 액체기둥이 주위의 액체면 보다 내려가게 됩니다. 수은이 대표적인 예시입니다(대략 접촉각은 $\theta \approx 130^{\circ}$, 깨끗한 유리). 당연하겠지만 접촉각은 $90^{\circ}$ 보다 큽니다.
즉,
(부착력>응집력) : 접촉각 0~90도 사이
(부착력<응집력) : 접촉각 90~180도 사이
입니다!
예제를 풀고 마무리합시다.
Ex1 ) 깨끗한 유리관을 $20^{\circ} \mathrm{C}$ 의 물이 모세관현상에 의해 올라가는 높이가 $h=1.0 \mathrm{~mm}$ 이하가 되도록 하려면 튜브의 직경은 얼마가 되어야 하는가?
참고 : $20^{\circ} \mathrm{C}$ 인 물의 경우, $\sigma=0.0728 \mathrm{~N} / \mathrm{m}$ 이 고 $\gamma=9.789 \mathrm{kN} / \mathrm{m}^3$ 이다. 물의 접촉각은 $\theta \approx 0^{\circ}$이다.
더보기를 눌러 해설을 보실 수 있습니다. 먼저 풀어보시기 바랍니다.
Sol.
직경을 구하려면 먼저 $R$에 대해 표현해야 합니다.
위 식으로부터
$$
h=\frac{2 \sigma \cos \theta}{\gamma R}
$$
이므로 $R$에 대해 표현하면
$$
R=\frac{2 \sigma \cos \theta}{\gamma h}
$$
입니다.
접촉각$\theta \approx 0^{\circ}$ 이므로 $h=1.0 \mathrm{~mm}$ 에 대해서는
주어진 수치를 모두 대입하면 됩니다.(미터 단위로 고치는 것을 잊지 맙시다!)
$$
\begin{aligned}
R & =\frac{2(0.0728 \mathrm{~N} / \mathrm{m})(1)}{\left(9.789 \times 10^3 \mathrm{~N} / \mathrm{m}^3\right)(1.0 \mathrm{~mm})\left(10^{-3} \mathrm{~m} / \mathrm{mm}\right)} \\
& =0.0149 \mathrm{~m}
\end{aligned}
$$
이고 필요한 최소 직경 $D$ 는
$$
D=2 R=0.0298 \mathrm{~m}=29.8 \mathrm{~mm}
$$
가 됩니다. (직경은 지름을 말합니다.!)
읽어주셔서 감사합니다! 이것으로 1단원이 모두 끝났습니다.
2단원에서는 미분적분학의 다양한 개념을 사용해야 합니다. 제 블로그에도 미적분학 포스팅이 올라가 있으니 참고하시어 다음 단원도 힘내봅시다!
이전 강의 보기
[유체역학 개념정리] 1.4 유체의 압축성(등엔트로피 압축), 체적계수, 음속(incompressible, bulk modulus,
목차1. 유체의 압축성(compressibility)체적계수와 비압축성등온과정과 등엔트로피과정에서의 체적계수2. 음속(Speed of sound)음속 시작하기 전에..유체역학을 처음 배우는 분들, 유체역학을 다시 보고
azale.tistory.com
다음 강의 보기
고난도 문제풀이
2024.08.09 - [고전역학/유체역학] - [유체역학 개념정리] 1단원 문제풀이
[유체역학 개념정리] 1단원 문제풀이
시작하기 전에..유체역학을 처음 배우는 분들, 유체역학을 다시 보고 싶으신 분들, 혹은 유체역학에 대해 알고 싶어서 오신 분들 환영합니다!저는 대학에 다니고 있는 대학생으로, 제가 공부했
azale.tistory.com
