목차
1.이변수함수(Functions of Two Variables)
2.그래프(Graph)와 등위곡선(Level Curve)
3.삼변수함수, $n$변수함수
4. 예제
증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니다.
이변수함수(Functions of Two Variables)
지금까지 우리가 배웠던 함수들은 모두 단 한개의 변수를 가진 함수들이었습니다.
즉, $y=f(x)$에서 $x$ 한 개만 가지고 있는 함수들을 다루었죠.
이제 드디어 우리는 미분적분학의 꽃인 이변수함수에 대해 배울 것입니다.
사실 변수의 개수는 늘리고 싶은 만큼 늘릴 수 있지만 미분적분학에서는 2,3변수함수까지만 다룹니다.
Def. 이변수함수
이변수함수(function $f$ of two variables) $f$ 는 집합 $D$ 에 속하는 각 실수의 순서 쌍 $(x, y)$ 에 대해 $f(x, y)$ 로 표시되는 유일한 실수를 대응시키는 규칙이다. 이때 집합 $D$ 는 $f$ 의 정의역이고, $f$ 의 치역은 $f$ 가 취하는 값들의 집합, 즉 $\{f(x, y) \mid(x, y) \in D\}$ 이다.
말이 좀 어려운데 쉽게 풀어서 말하자면 변수를 하나가 아니라 두 개 가지고 있는 함수를 말합니다.
즉, $x, y$ 두 개의 값에 영향을 받는 함수라고 생각하시면 됩니다.
보통 이변수함수는 표기할 때 대부분의 경우에서 $z=f(x, y)$ 로 씁니다.
이때 변수 $x$ 와 $y$ 는 독립변수고, $z$ 는 종속변수입니다.
함숫값을 구할 때는 그냥 $x$, $y$ 자리에 해당하는 값을 넣으면 됩니다.
만약 $f(3, 2)$ 를 구하고 싶으면 $x$자리에 $3$, $y$자리에 $2$를 넣으면 끝입니다.
그럼 이변수함수를 이해할 때는 어떻게 이해하는게 좋을 까요?
먼저 기존에 배웠던 함수 $y=f(x)$는 가로축을 $x$, 세로축을 $y$로 두었습니다.
그런데 이번엔 문자가 3개라서, 좌표평면에 나타내기에는 한계가 있습니다.
예상하셨겠지만, "3차원 좌표계", 즉 "공간좌표계"를 도입합니다.

위 그림은 일반적인 경우의 이변수함수입니다.
앞서 말했듯이 독립변수가 $x, y$로 2개이므로, 축을 두 개 사용하여 나타냅니다.
그리고 함숫값(종속변수, 또는 치역)은 $z$인데, 이미 평면상에서는 모든 변수를 사용했으니까 높이, 즉 기존의 $z$축을 함숫값으로 사용합니다.
위 그림에서도 알 수 있듯이, 이변수함수는 정의역으로 $x, y$ 2 개를 사용하므로 정의역이 $\mathbb{R}^2$ 의 부분집합입니다.
치역은 한 개의 축 $z$축으로만 이루어져있으므로, $\mathbb{R}$ 의 부분집합입니다.
그림에서도 알 수 있듯이 정의역이 $\mathbb{R}^2$라는 말은 곧 정의역이 "영역"으로 표시된다는 말과 동치입니다.
밑의 예제에서도 볼 수 있지만 대략 이렇게 표시됩니다.
아래 그림은 $f(x, y)=x \ln \left(y^2-x\right)$ 의 정의역입니다.

그래프(Graph)와 등위곡선(Level Curve)
앞에서 이변수함수의 정의역이 2차원 평면 형태로 그려진다고 알아보았습니다.
그러면, 공간좌표계 내에서 3차원 형태로 표현할 수도 있지 않을까요?
정의역과 치역을 연결시켜서 공간좌표 위에 나타낸 것을 그래프(Graph)라고 합니다.

Def. 그래프(Graph)
$f$ 가 정의역 $D$ 인 이변수함수이면, $f$ 의 그래프는 $(x, y)$ 가 $D$ 에 속하고 $z=f(x, y)$ 인 $\mathbb{R}^3$ 에 속하는 점 $(x, y, z)$ 전체의 집합이다.
풀어서 말하자면 앞에서 보았던 $z=f(x, y)$를 통해서 곡면을 그린 것이라고 생각하면 됩니다.
이변수함수를 시각화할 수 있는 가장 좋은 방법이라고 말할 수 있습니다.
보통 그래프를 그리라는 문제를 보면 그냥 $f(x, y)=z$ 로 두고 3차원에서 도형의 형상을 생각하면 됩니다. 밑의 예제에서 확인할 수 있습니다.
그렇지만 우리가 시험을 컴퓨터를 통해 보는 것도 아니기에, 조금 더 이변수함수를 쉽게 표현할 수 없을까요?
이변수함수를 $z$값을 포함해서 2차원 평면상에 적절히 나타내는 방법이 있는데, 이는 등위곡선(Level Curve)입니다.
아마 여러분들도 등고선 지도를 본 적이 있으실 텐데, 다 이 기법을 활용한 겁니다.

Def. 등위곡선(Level Curve)
등위곡선 $f(x, y)=k$ 는 $f$ 가 주어진 값 $k$ 를 취하는 $f$ 의 정의역에 속한 점 전체의
집합이다.
즉, 이는 $f$ 의 그래프에서 높이 $k$ 인 곳을 보여 준다.
즉, 2차원 평면 위에, 함숫값이 같은 점들끼리 이어서 곡선을 만든 것이라고 생각하시면 됩니다.
이걸 계속 이으면 등위곡선이 됩니다.
예제에서 등위곡선과 관련된 문제를 확인할 수 있습니다.
삼변수함수, $n$변수함수
이변수함수가 있으면 당연히 변수의 개수를 늘려서 삼변수함수도 있겠죠..?
다행인 점은 삼변수함수부터는 손으로 계산하기가 어려워서 시험에 잘 나오지 않는다는 점입니다.
그래도 어떤 건지는 알아두는게 좋으니 한번 같이 살펴봅시다!
Def. 삼변수함수
삼변수함수(function of three variables) $f$ 는 정의역 $D \subset \mathbb{R}^3$ 에 속하는 세 순서쌍 $(x, y, z)$ 에 대해 $f(x, y, z)$ 로 표기되는 유일한 실수를 대응시키는 규칙이다.
정의는 어렵게 써놓았지만 결국 함수의 정의이고, 앞의 이변수함수에서 그냥 변수 한 개가 더 추가된 것이라고 생각하시면 됩니다.
아쉽게도(?) 삼변수함수는 그리기가 정말 어려워서, 시험에 잘 나오지 않습니다.
삼변수함수는 4차원 공간에 있으므로 그래프로 시각화하기 정말 어렵지만, 등위곡면(level surface)을 활용하면, 어떻게 표현은 가능합니다.
(앞과 마찬가지로 상수 $k$ 에 대해 방징식 $f(x, y, z)=k$ 를 생각하시면 됩니다!)

이렇게 변수를 계속 확장시켜 가보면, 일반적인 $n$변수함수를 정의할 수 있게 됩니다.
Def. $n$변수함수(function of $n$ variables)
$n$변수함수는 실수의 $n$-순서쌍 $\left(x_1, x_2, \ldots, x_n\right)$ 에 수 $z=f\left(x_1, x_2, \ldots, x_n\right)$ 을 대응시키는 규칙이다. 이러한 $n$-순서쌍 전체의 집합을 $\mathbb{P}^n$ 으로 나타낸다
가령 어떤 회사가 제품들을 만드는 데 $n$ 개의 서로 다른 재료를 쓴다고 해봅시다.
$c_i$ 를 $i$ 번쩨 재료의 단위당 가격, $i$ 번쩨 재료를 $x_i$번 이용한다면,
재료를 구입할 때 소요되는 충 비용 $C$ 는 다음 과. 같이 $n$ 변수 $x_1, x_2, \ldots, x_n$ 의 함수로 나타낼 수 있습니다.
$$
C=f\left(x_1, x_2, \ldots, x_n\right)=c_1 x_1+c_2 x_2+\cdots+c_n x_n
$$
이렇게 변수가 많은 함수도 사용될 수 있습니다.
$n$변수함수는 사실 수학과가 아니라면 그렇게 중요하지 않으니 그냥 넘기셔도 됩니다 :)
예제
P1(이변수함수).
다음 각 함수에서 $f(3,2)$ 의 값을 계산하고, 정의역을 구하고 정의역의 그림을 그리시오.
(a) $$f(x, y)=\frac{\sqrt{x+y+1}}{x-1}$$
(b) $$f(x, y)=x \ln \left(y^2-x\right)$$
(a)
함숫값은 그냥 대입하면 됩니다.
$$f(3,2)=\frac{\sqrt{3+2+1}}{3-1}=\frac{\sqrt{6}}{2}$$
정의역을 따질 때 중요한 부분들이 여러 개 있었죠.
이 함수에서 볼 것들은
1.분모가 0이 아니다.
2.제곱근 안의 부호가 음이 아니어야 한다.
이 두 가지만 보면 되겠네요.
그러므로 $f$ 의 정의역은 다음과 같습니다.
$$
D=\{(x, y) \mid x+y+1 \geq 0, x \neq 1\}
$$
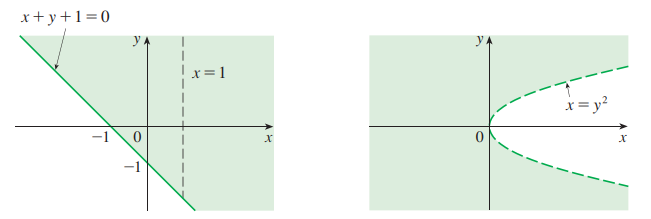
부등식 $x+y+1 \geq 0$를 $xy$평면에 대해서 풀어봅시다.
그렇게 되면 $y \geq-x-1$이고 이는 $y=-x-1$ 또는 그보다 위에 있는 점들을 나타냅니다.
그리고 $x \neq 1$ 을 이후에 고려하면 됩니다.
(b)
아까 했던 대로 함숫값을 계산하면 $f(3,2)=3 \ln \left(2^2-3\right)=3 \ln 1=0$ 입니다.
로그함수에서 정의역 조건을 잘 생각해봅시다.
$\ln \left(y^2-x\right)$ 는 $y^2-x>0$ 일 때, 즉 $x<y^2$ 일 때 정의됩니다.
따라서 $f$ 의 정의역은
$$D=\left\{(x, y) \mid x<y^2\right\}$$
입니다.
잘 이해해 보면 이는 포물선 $x=y^2$ 의 왼쪽에 있는 점들의 집합입니다.
P2.이변수함수, 그래프
$g(x, y)=\sqrt{9-x^2-y^2}$ 의 정의역과 치역을 구하시오. 또한 그래프(Graph)도 구하시오.
풀이
$g$ 의 정의역, 루트함수의 정의에 의해 구할 수 있습니다. 즉,
$$
D=\left\{(x, y) \mid 9-x^2-y^2 \geq 0\right\}=\left\{(x, y) \mid x^2+y^2 \leq 9\right\}
$$
와 같습니다.
이때 여기서 $x^2+y^2 \leq 9$ 는 곧 중심이 $(0,0)$ 이고 반지름이 3 인 원판입니다.
$g(x, y)$를 $z$라고 하면, $g$ 의 치역은 다음과 같습니다.
$$
\left\{z \mid z=\sqrt{9-x^2-y^2},(x, y) \in D\right\}
$$
$z$ 는 양의 제곱근이기 때문에 $z \geq 0$ 입니다.
또한 $9-x^2-y^2 \leq 9$ 이므로,
$$
\sqrt{9-x^2-y^2} \leq 3
$$
으로부터 치역은 다음과 같습니다.
$$
\{z \mid 0 \leq z \leq 3\}=[0,3]
$$
그래프 문제는 위의 개념에서도 언급드렸듯이 그냥 $f$를 $z$로 바꾸고 3차원 공간에서 생각하시면 됩니다.
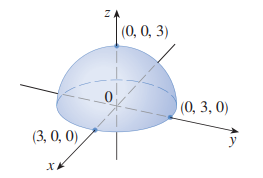
따라서 $g$ 의 그래프의 방정식은 $z=\sqrt{9-x^2-y^2}$ 입니다.
이때 이 방정식의 양변을 제곱해서 $z^2=9-x^2-y^2$, 즉 구의 방정식인 $x^2+y^2+z^2=9$ 를 얻을 수 있습니다.
이것은 중심이 원점이고 반지름이 3 인 구의 방정식입니다.
다만 조심해야 할 점은 제곱 전에 $z$가 항상 양수, 즉 치역이 항상 양수였으니,
$z \geq 0$ 이므로 $g$ 의 그래프는 구의 위쪽 반이 됩니다.
P3) $x>0, y>0, z>0$인 제1팔분공간에서 함수 $f(x, y)=6-3 x-2 y$ 의 그래프를 그리시오.
그래프 문제는 위의 개념에서도 언급드렸듯이 그냥 $f$를 $z$로 바꾸고 3차원 공간에서 생각하시면 됩니다.
$f$ 의 그래프의 방정식은 $z=6-3 x-2$ 또는 $3 x+2 y+z=6$ 이며 평면입니다.
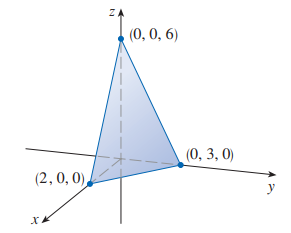
평면을 그리기 위해서는 먼저 절편을 구해야 합니다.
방정식에서 $y=z=0$ 로 놓으면 $x$ 절편 2 를 얻습니다.
마찬가지로 계산하면. $y$ 절편은 $3, z$ 절편은 6입니다.
그림을 그리면 아래와 같습니다.
P4. (등위곡선, level curve)
함수 $f(x, y)=6-3 x-2 y$ 의 등위곡선을 그리시오.
(이때 $k=-6,0,6,12$ 의 등위선만 그릴 것)
등위곡선은 그냥 $f$를 $k$로 놓으면 됩니다. 그렇게 하여 식을 정리하면
$$
6-3 x-2 y=k
$$
$$
3 x+2 y+(k-6)=0
$$
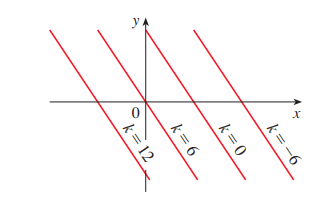
이는 기울기가 $-\frac{3}{2}$ 인 직선임을 알 수 있습니다.
주어진 $k$값을 대입하면, $k=-6,0,6,12$ 일 때 각각 $3 x+2 y-12=0$, $3 x+2 y-6=0,3 x+2 y=0,3 x+2 y+6=0$ 입니다.
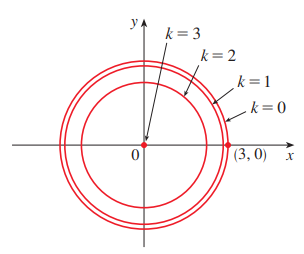
P5. (등위곡선, level curve)
함수 $g(x, y)=\sqrt{9-x^2-y^2}$ 의 등위곡선을 그려시오.
($k=0,1,2,3$의 등위선만 그릴 것)
등위곡선은 그냥 $f$를 $k$로 놓으면 됩니다. 식을 정리하면
$$
\sqrt{9-x^2-y^2}=k, x^2+y^2=9-k^2
$$
이는 중심이 $(0,0)$ 이고 반지름이 $\sqrt{9-k^2}$ 인 원의 방정식입니다.
주어진 $k$값은 루트의 정의에 어긋나지 않으므로 대입할 수 있습니다!
$k=0,1,2,3$ 일 때 등위 곡선은 아래 그림과 같습니다.
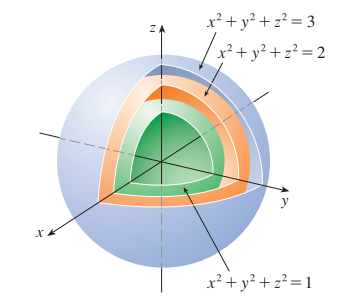
P6. 삼변수함수
함수 $f(x, y, z)=x^2+y^2+z^2$ 등위곡면(level surface)을 구하시오.
($k=1,4,9$의 등위면만 그릴 것, 3차원 공간에 그릴 것)
등위곡면은 등위곡선과 같이 $f$를 $k$로 바꾸면 됩니다.
다만 "그리기"에는 매우 까다롭습니다. 그래서 여러 $k$값을 대입해서 대략적인 형상을 생각하는 것입니다.
먼저 등위곡면은 $x^2+y^2+z^2=k(k \geq 0)$ 입니다.
이는 반지름이 $\sqrt{k}$ 인 구입니다.
$k$의 각 값들을 대입해서 그리면 아래와 같습니다.
감사합니다.
다음 시간에는 이변수함수의 극한과 연속에 대해 알아보겠습니다.
이전 게시물 보기
[미분적분학(2) 개념 정리] 12.3 (2) 단위법선벡터, 종법선벡터, 곡률원, 비틀림율 (principal unit normal
목차1. 주단위법선벡터 $\mathbf{N}$, 종법선벡터 $\mathbf{B}$2. 곡률원3. 비틀림율(torsion)4. 예제증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니다.주단위법선벡터(principa
azale.tistory.com
다음 게시물 보기
13.2 이변수함수의 극한과 연속(Limits and continuity of Functions of Two Variables)
목차1.이변수함수의 극한 (Limits of Functions of Two Variables) 2.이변수함수의 연속 (continuity of Functions of Two Variables) 3.예제증명이나 해설은 더보기를 눌러 확인할 수 있습니다! 꼭 한번씩 보시기 바랍니
azale.tistory.com



